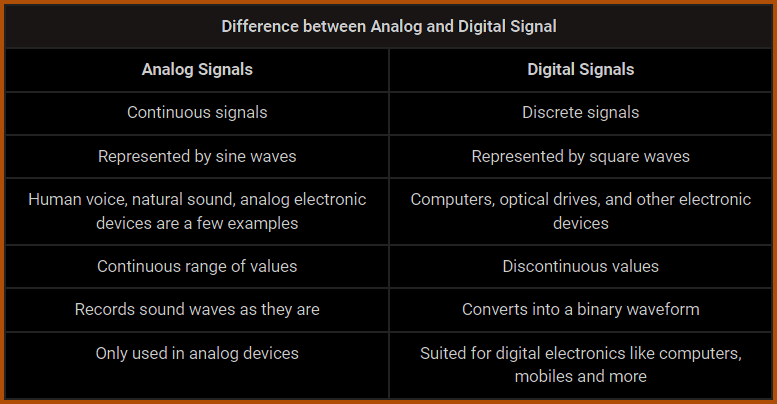
In analog technology, a wave is recorded or used in its original form. So, for example, in an analog tape recorder, a signal is taken straight from the microphone and laid onto tape. The wave from the microphone is an analog wave, and therefore the wave on the tape is analog as well. That wave on the tape can be read, amplified and sent to a speaker to produce the sound.
In digital technology, the analog wave is sampled at some interval, and then turned into numbers that are stored in the digital device. On a CD, the sampling rate is 44,000 samples per second. So on a CD, there are 44,000 numbers stored per second of music. To hear the music, the numbers are turned into a voltage wave that approximates the original wave.
The two big advantages of digital technology are:
1. The recording does not degrade over time. As long as the numbers can be read, we will always get exactly the same wave.
2. Groups of numbers can often be compressed by finding patterns in them. It is also easy to use special computers called digital signal processors (DSPs) to process and modify streams of numbers.
Representing Data Digitally
Computers store all data as bits: positive numbers, negative numbers, fractional numbers, text, colors, images, audio and video, etc.
Let's now consider how various types of data might be represented using binary.
Digital Text
In the context of computing, text means a collection of alphanumeric and related symbols, also called characters. Text is usually used to represent words, sentences, paragraphs, and so forth and does not include various formatting, such as underline, bold, italic and so on. We will limit our character set to the English alphabet and related characters.
So we need A through Z, uppercase and lowercase, meaning A is a different symbol than a. We also want punctuation marks like commas and periods. We need a way to represent spaces. We also need digits 0 through 9. If we add up all the unique symbols we need to represent, we have around 100 characters, that we can represent with a 7-bit number (128 combinations, 27), but since computers usually work in bytes, it makes sense to just round up and use a full 8 bits, one byte, to represent each character. With a byte we can represent 256 unique characters.
There is already a standard way of representing text in binary, but for now, if you imagine that you are responsible for creating your own system that represents each character as a set of bits, you might, let's say, decide to assign 0b00000000 to represent character A, and 0b00000001 to represent character B, and so on. This process of translating data into a digital format is known as encoding; when you interpret that digital data, we talk about decoding.
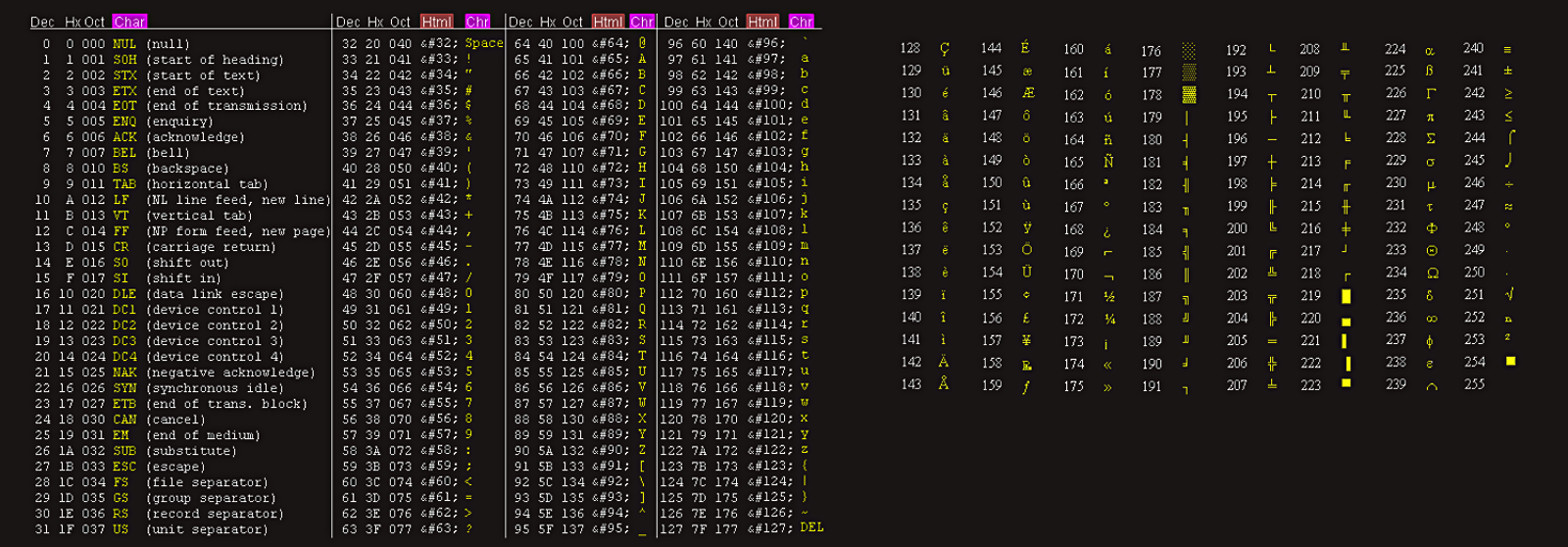
ASCII
As we have said, and earlier explained, we already have several standard ways to represent text digitally, so we don’t have to invent our own. American Standard Code for Information Interchange (ASCII) is a format that represents 128 characters using 7 bits per character, although each character is commonly stored using a full byte, 8 bits. Using 8 bits instead of 7 just means we have an extra leading bit, left as 0.
ASCII handles the characters needed for English, and another standard, called Unicode, handles characters used in nearly all languages, with English included.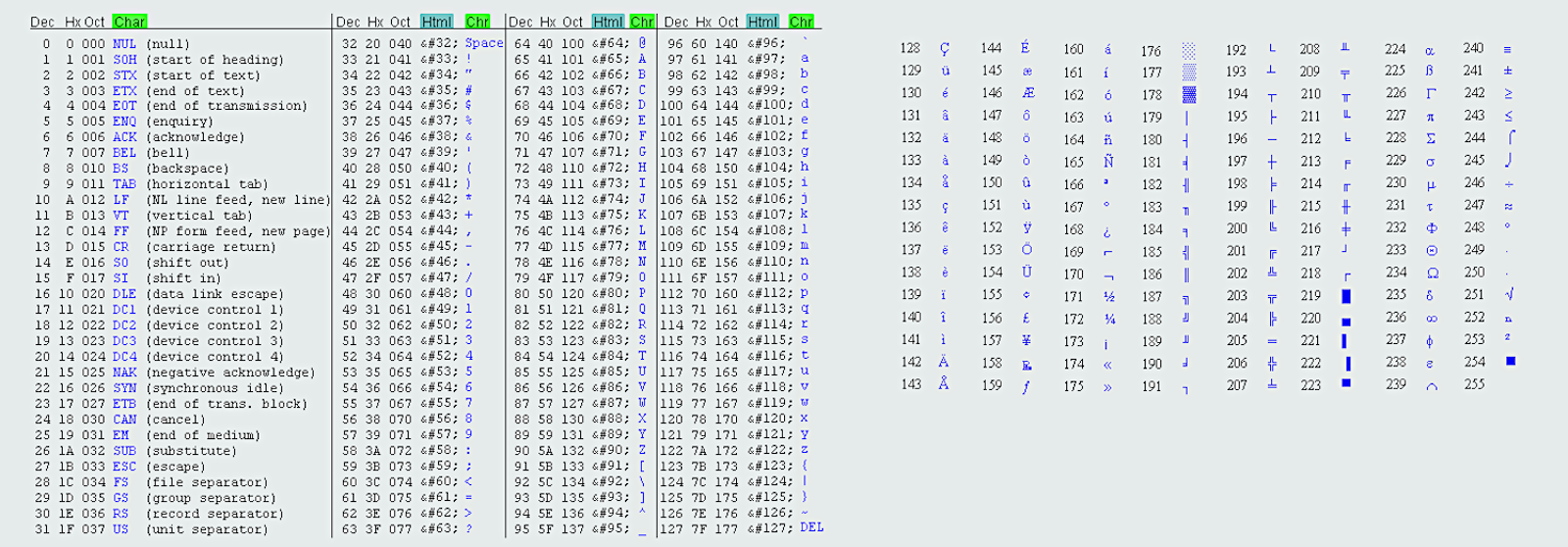
A system like ASCII maps each character, or symbol, to a unique sequence of bits. A computing device then interprets that sequence of bits and displays the appropriate symbol to the user. Binary representation is not displayed in the table above.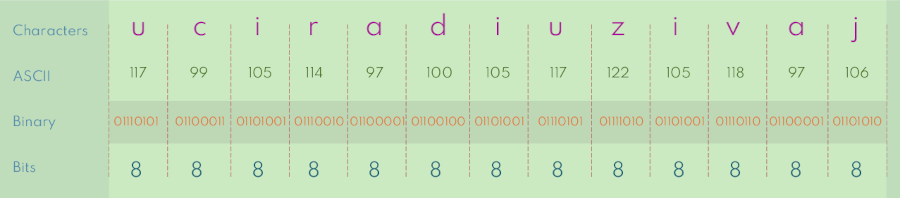
Digital Colors and Images
As it is with text mentioned above, there are standard ways of storing color data, also. We will now first design our own system for digitally describing colors, and limit our range of colors to black, white, and shades of gray, and to keep it simple in this grayscale we will only go with black, white, dark gray, and light gray. Here we have only 4 colors, and to represent those colors, we only need 2 bits, 22 = 4. So now, we can get a simple grayscale image. What is an image? An image is essentially an arrangement of colors on a two-dimensional plane. Those colors are typically arranged in a grid composed of single-color squares called pixels.
In the image above, we could think of each pixel as being represented by a 0 (black) or 1 (white), so it could be stored as a binary string of 36 bits: 111111101101111111101101100001111111. To successfully draw the image from that pattern, we would have to know to interpret those series of binary digits as 6 rows of 6 pixels (and not say 4 rows of 9 pixels), so real image file formats often include extra information like the dimension of the image.
In this example, to illustrate a point, we have shown some really large pixels, and we should have in mind that modern televisions, computer monitors, and smartphone screens can also be thought of as a grid of pixels, but each pixel is very small. For example, a high definition display is typically 1920 pixels (width) by 1080 pixels (height), for a total of about 2 million pixels! As another example, digital photographs often contain more than 10 million pixels in a single image.
In images, we often want to represent shades of gray or colors. To do so, each pixel can be assigned more than one bit. If each pixel is given a value consisting of 2 bits we can have 4 colors, like we have already mentioned above:
· 00 black
· 01 dark gray
· 10 light gray
· 11 white
And now to draw the image from the bits we would need to know the dimensions of the image; but also we would need to specify the number of bits used for each pixel, for example we could make a shaded circle.
A pattern of bits only has the meaning we assign to it. So, 32 bits could represent a 4x8 image of 1-bit pixels, or a 4x4 image of 2-bit pixels, or a sequence of 4 ASCII letters, or a really large binary number, or nearly anything else.
Because bits only have the meaning we assign to them, we could interpret the 2 bits per pixel to mean some other colors, for example: red, orange, yellow, white and we would get colored image. If we want more than 4 colors, we just need more than 2 bits. With 8 bits per pixel, we can represent 28 = 256 different colors or shades of gray. This is sufficient for a black and white photograph but does not allow for subtle shades of color in a photograph. For full color images, 24 bits are usually used per pixel, allowing for 224 = 16.777.216 different colors. Real images, of course, use a much greater number of pixels than we have seen here. For example, a 12-megapixel camera takes images that measure about 4000x3000 pixels. If each of those pixels is stored as a 24-bit value, that image would consist of 4000 x 3000 x 24 = 288.000.000 bits of information!