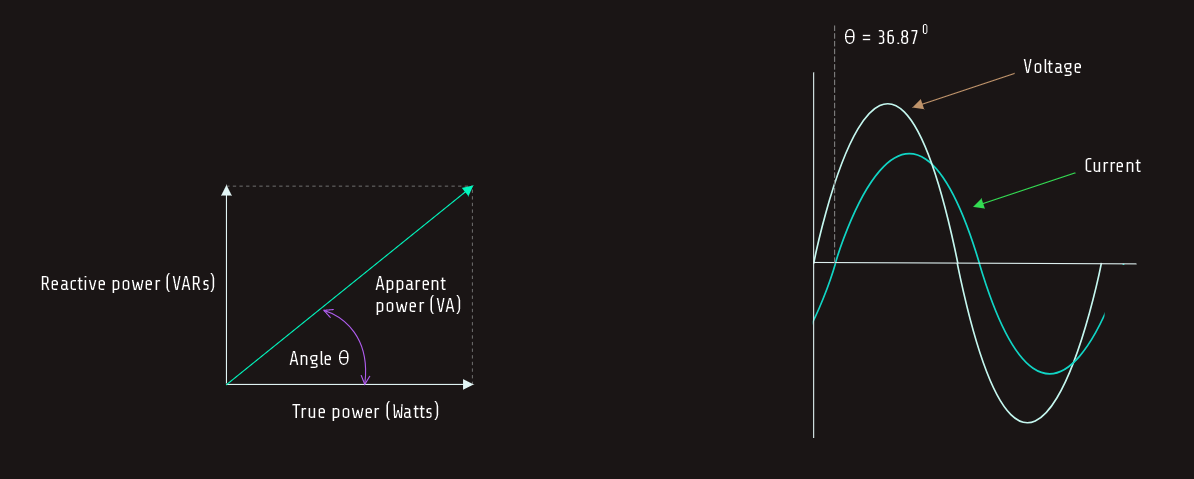
Angle Theta
The cosine of angle theta (cos ∠θ) is equal to the power factor.
cos ∠θ = 0,80
θ = 36,870 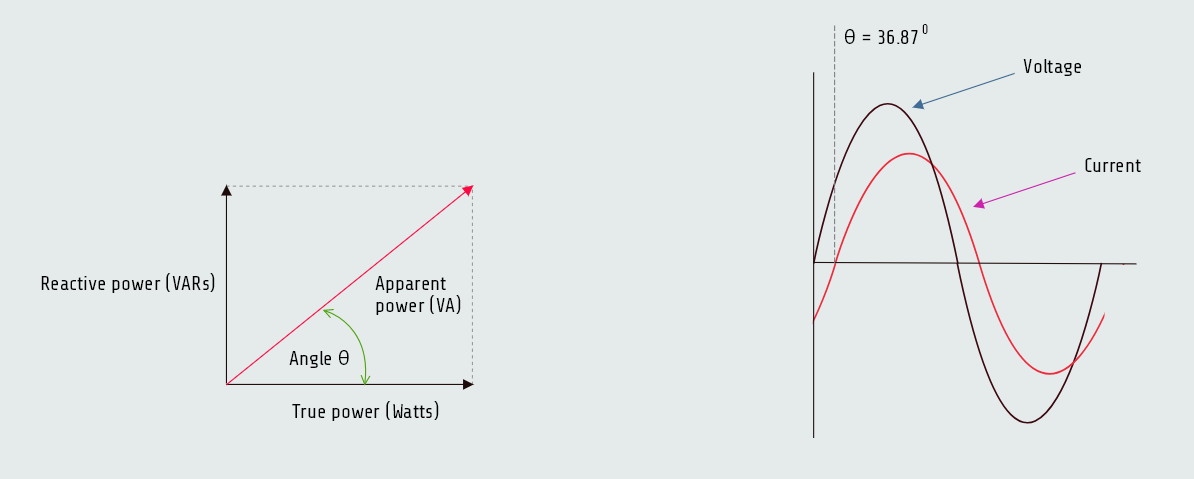
Capacitance in AC circuits
Capacitors perform a variety of jobs such as power factor correction, storing an electric charge to produce a large current pulse, timing circuits, and electronic filters. Capacitors can be nonpolarized or polarized depending on the application and discussed later on.
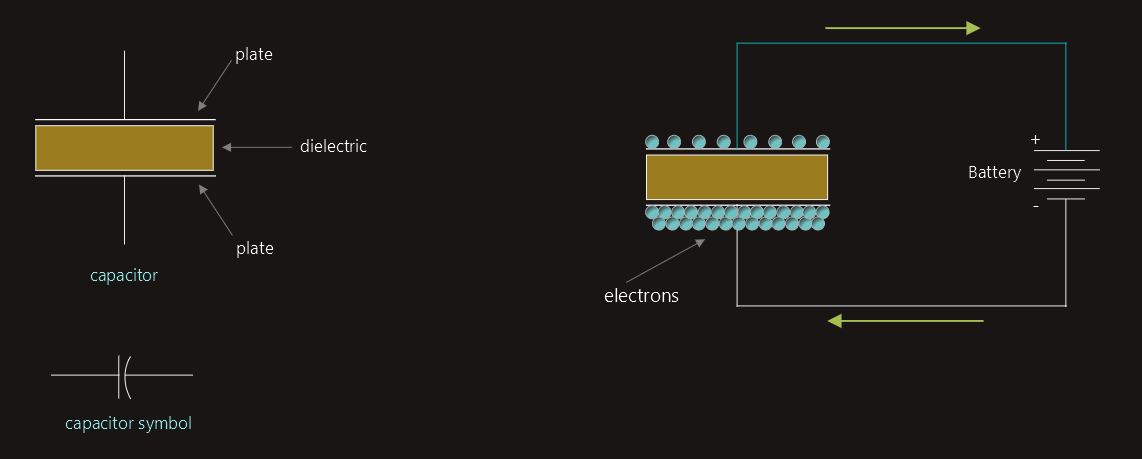
Capacitors are devices that oppose a change of voltage.
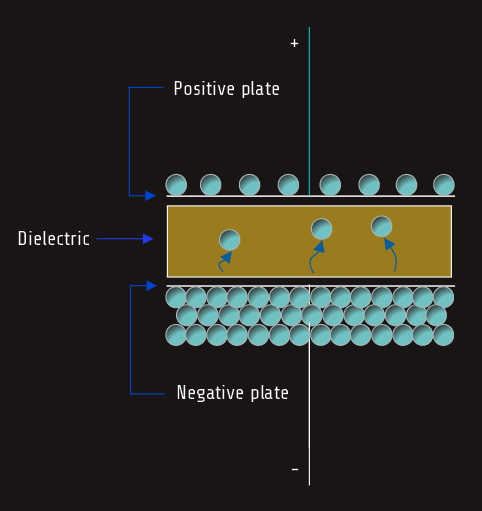
The simplest type of capacitor is constructed by separating two metal plates by some type of insulating material called the dielectric. 
Electrostatic charge
We know by now that there are three factors that determine the capacitance of the capacitors, one of them is the surface area of the plates - the greater the surface area of the plates, the more capacitance a capacitor will have. To understand other two factors, the type of dielectric used and the distance between the plates, it is necessary to understand how a capacitor stores energy.
It was discussed earlier that an inductor stores energy in the form of a magnetic field. A capacitor stores energy in an electrostatic field.
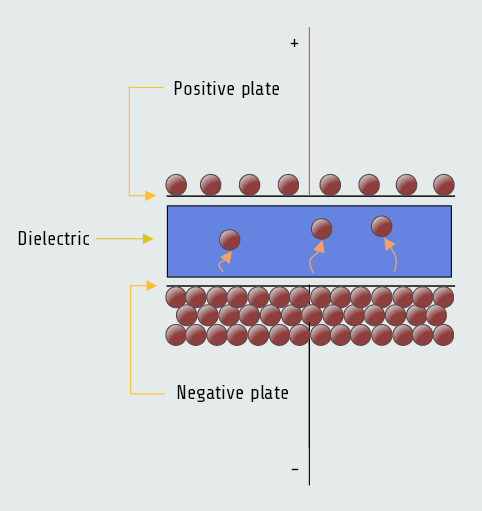
The term "electrostatic" refers to electric charges that are stationary, or not moving. They are very similar to the static electric charges that form on objects that are good insulators. The electrostatic field is formed when electrons are removed from one plate and deposited on the other.
When a capacitor is not charged, the atoms of the dielectric are uniform. The valence electrons orbit the nucleus in a circular pattern. When the capacitor becomes charged, however, a potential exists between the plates of the capacitor. The plate with the lack of electrons has a positive charge, and the plate with the excess of electrons has a negative charge. Since electrons are negative particles, they are repelled away from the negative plate and attracted to the positive plate. This attraction causes the electron orbit to become stretched, and this stretching of the atoms of the dielectric is called dielectric stress.
Placing the atoms of the dielectric under stress has the same effect as drawing back a bowstring with an arrow and holding it - that is, it stores energy.
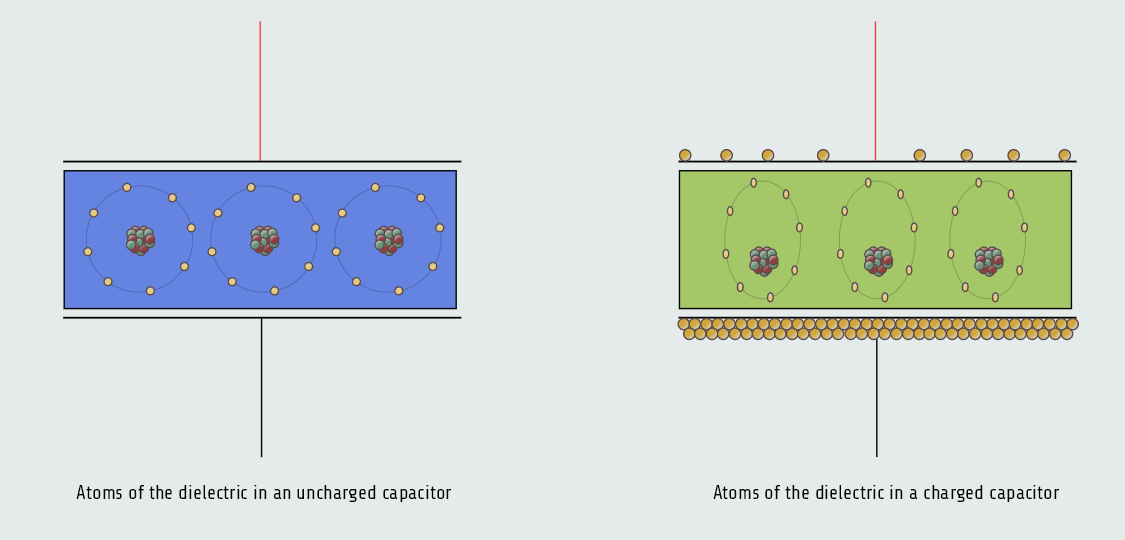
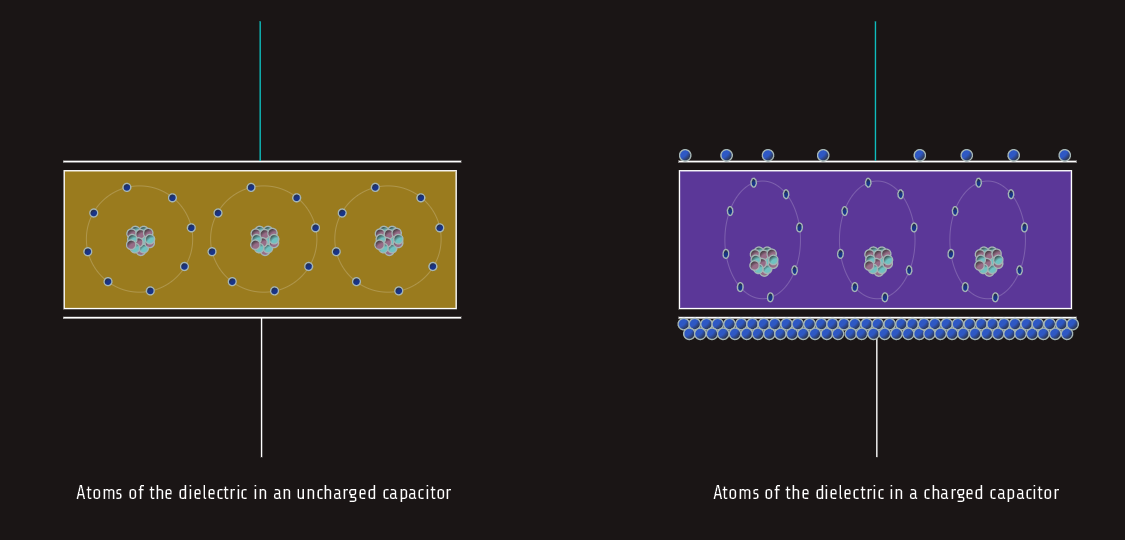
The amount of dielectric stress is proportional to the voltage difference between the plates. The greater the voltage, the greater the dielectric stress. If the voltage becomes too great, the dielectric will break down and permit current to flow between the plates. At this point the capacitor becomes shorted. Capacitors have a voltage rating that should not be exceeded. The voltage rating indicates the maximum amount of voltage the dielectric is intended to withstand without breaking down.
The energy of the capacitor is stored in the dielectric in the form of an electrostatic charge.
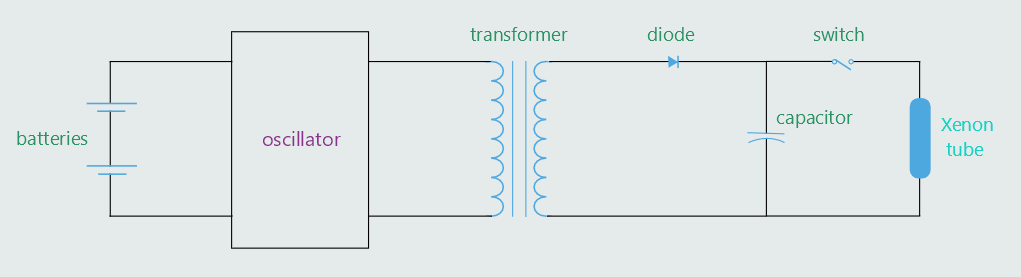
It is this electrostatic charge that permits the capacitor to produce extremely high currents under certain conditions. If the leads of a capacitor are shorted together, it has the effect of releasing the drawn-back bowstring, compared above. When the bowstring is released, the arrow is propelled forward at a high rate of speed. The same is true for the capacitor. When the leads are shorted, the atoms of the dielectric snap back to their normal position. Shorting causes the electrons on the negative plate to be literally blown off and attracted to the positive plate. Capacitors can produce currents of thousands of amperes for short periods of time.
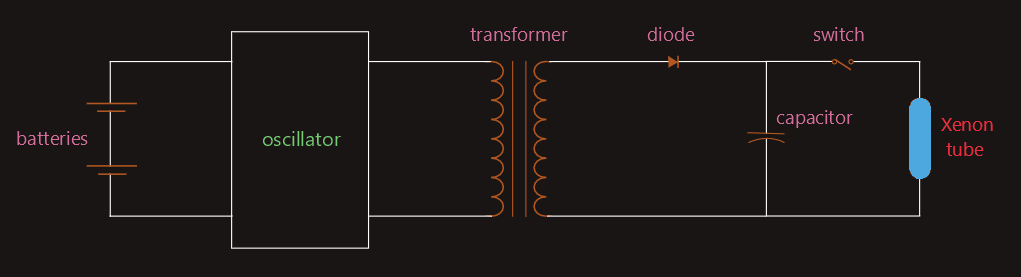
This principle, for example, is used to operate the electronic flash of many cameras. Electronic flash attachments contain a small glass tube filled with a gas called xenon, that produces a very bright white light similar to sunlight when the gas is ionized. We have already shown this example in circuit analysis of the following circuit:
Dielectric constant
Since much of the capacitor’s energy is stored in the dielectric, the type of dielectric used is extremely important in determining the amount of capacitance a capacitor will have. Different materials are assigned a number called the dielectric constant. Vacuum is assigned the number 1 and is used as a reference. Air, for example, has a dielectric constant of approximately 1.0006.
If we assume that a capacitor uses vacuum as the dielectric and it is found to have a capacitance of 1 microfarad (1 µF); then let's assume that some material is placed between the plates without changing the spacing and the capacitance value becomes 5 microfarad. So, this material has a dielectric constant of 5.
Capacitor ratings
The basic unit of capacitance is the farad (symbolized by the letter F). It receives its name from a famous scientist named Michael Faraday. A capacitor has a capacitance of one farad when a change of one volt across its plates results in a movement of one coulomb.
Q = CxV
· Q - charge in coulombs
· C - capacitance in farads
· V - charging voltage