Alternating Current
In DC circuits, the product of the current and voltage always equals the power or watts. We will find that this is not true in AC circuits, however, because the voltage and current can become out of phase with each other; which can be illustrated through the use of basic trigonometry through the next analysis.
Basic trigonometry and vectors
Many AC formulas are based on right triangles, because, depending on the type of load, the voltage and current in an AC circuit can be out of phase with each other by approximately 90 degrees. The exact amount of the out-of-phase condition is determined by different factors, which we will cover later on.
Right triangles
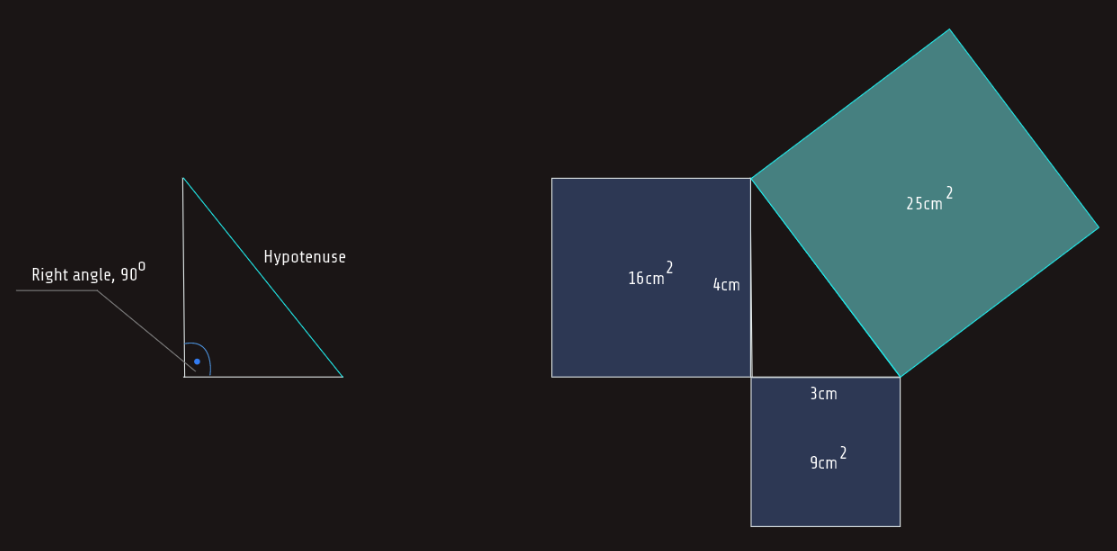
A right triangle is a triangle that contains a right or (90°) angle. The hypotenuse is the longest side of a right triangle and is always opposite the right angle.
Several thousand years ago, a Greek mathematician named Pythagoras made some interesting discoveries concerning triangles that contain right angles. One of these discoveries was that if the two sides of a right triangle are squared, their sum equals the square of the hypotenuse, following that hypotenuse is square-root of its area long. 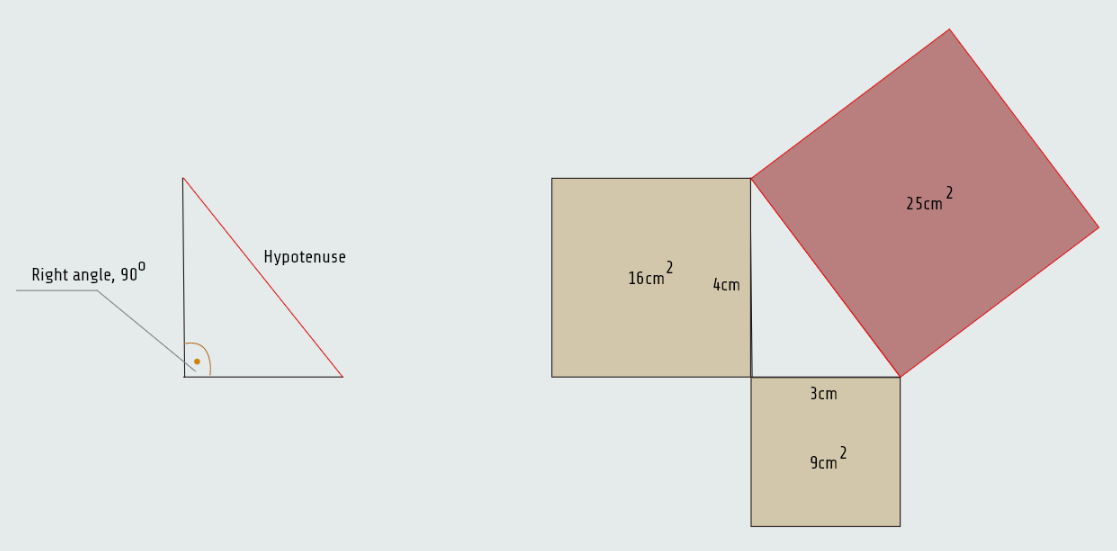
Pythagorean theorem
c2=a2+b2
c=√(a2+b2)
• c - the length of the hypotenuse
• a - the length of one side
• b - the length of the other side
Sines, cosines and tangents
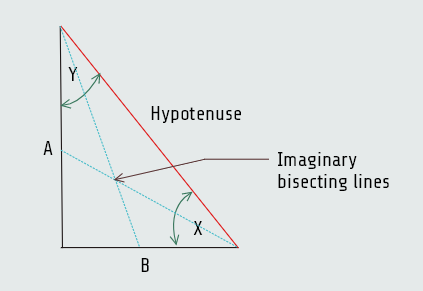
A second important concept concerning right triangles is the relationship of the length of the sides to the angles. Since one angle is always 90°, only the two angles that are not right angles are of concern. Another important fact concerning triangles is that the sum of the angles of any triangle equals 180°; since one angle of a right triangle is 90°, the sum of the two other angles must equal 90°.
It was discovered long ago that the number of degrees in each of these two angles is proportional to the lengths of the three sides. This relationship is expressed as the sine, cosine, or tangent of a particular angle. The hypotenuse is always the longest side of a right triangle, but the opposite and adjacent sides are determined by which of the two angles is to be found.
sine ∠ x = opposite/hypotenuse
cosine ∠ x = adjacent/hypotenuse
tangent ∠ x = opposite/adjacent
A side is opposite angle X, but adjacent to angle Y.
B side is opposite angle Y, but adjacent to angle X.
Vectors
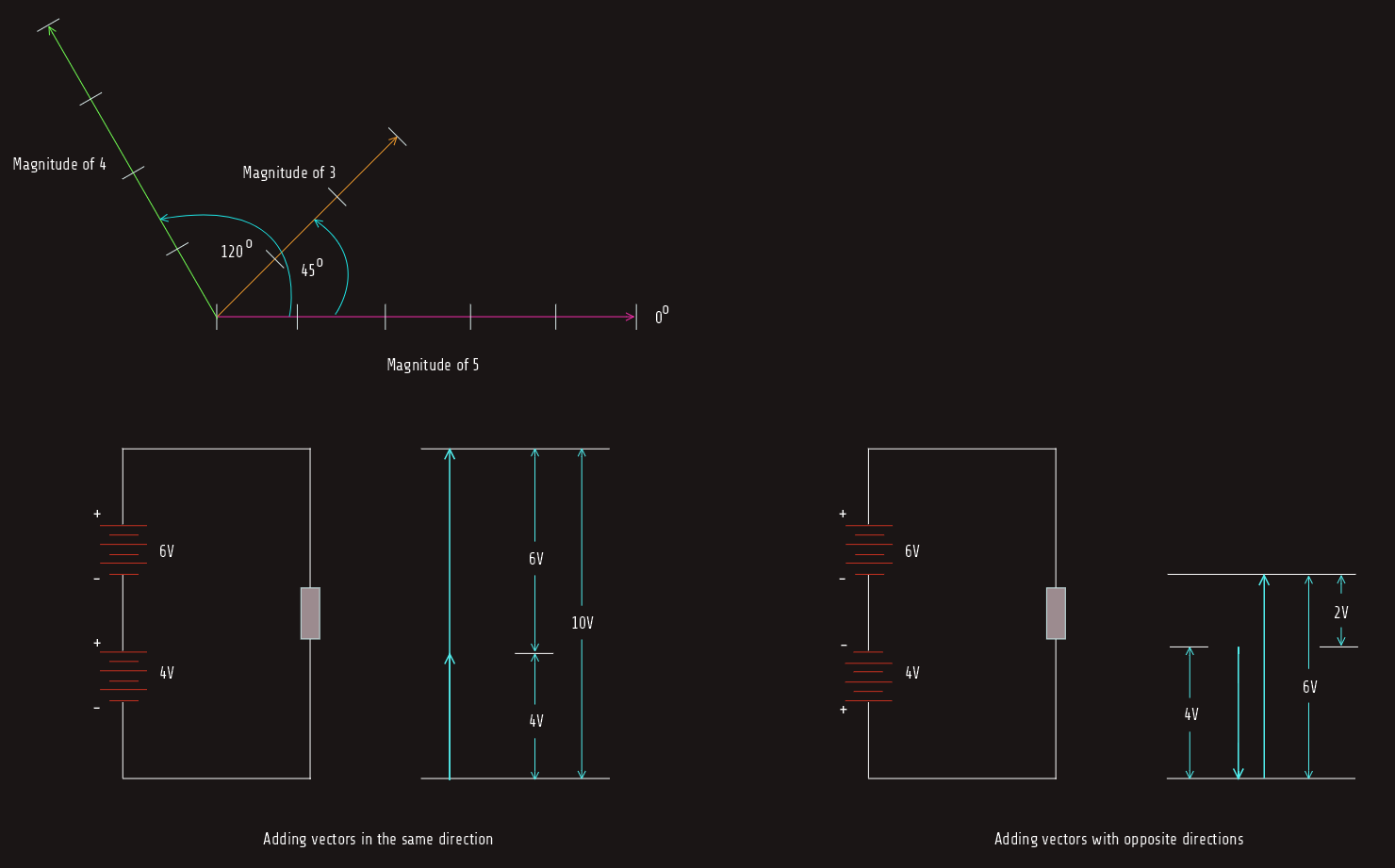
A vector is a line that indicates both magnitude and direction. The magnitude is indicated by its length, and the direction is indicated by its angle of rotation from 0°. Vectors should not be confused with scalars, which are used to represent magnitude only and do not take direction into consideration. Zero degrees is indicated by a horizontal line. An arrow is placed at one end of the line to indicate direction. The magnitude can represent any quantity such as inches, meters, miles, volts, amperes, ohms, power, and so on.
Here we have three vectors; a vector with a magnitude of 5 at an angle of 0°, a vector with a magnitude of 3 drawn at a 45° angle from the first vector and a vector with a magnitude of 4 drawn in a direction of 120° (referenced from the horizontal 0° line and not from the second vector line, which was drawn at an angle of 45°).
Because vectors are used to represent quantities such as volts, amperes, ohms, power, and so on, they can be added, subtracted, multiplied, and divided. In electrical work, however, addition is the only function needed. Several methods can be used to add vectors. Regardless of the method used, because vectors contain both magnitude and direction, they must be added with a combination of geometric and algebraic addition. This method is often referred to as vector addition.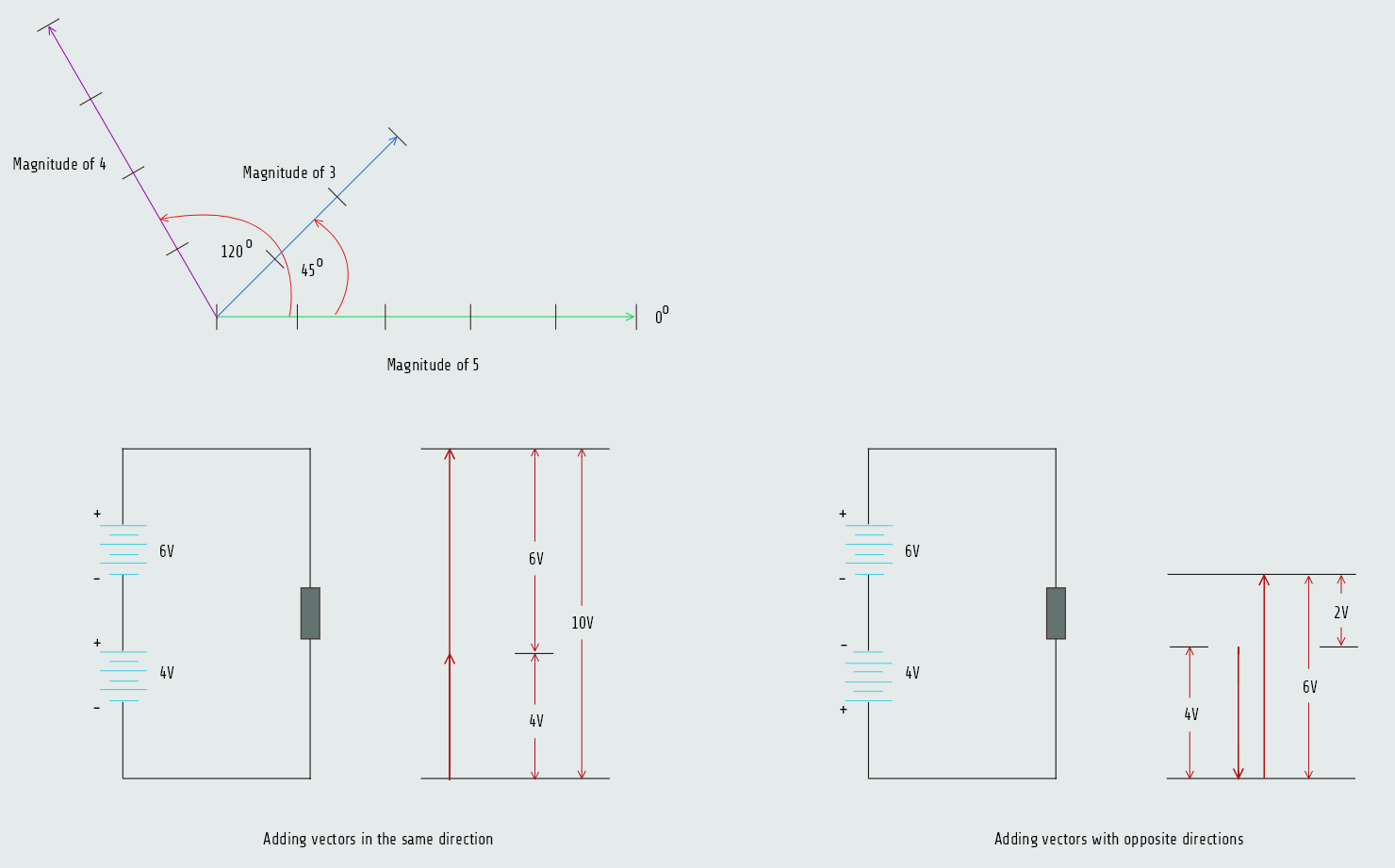
The addition of vectors of different directions is made by connecting the starting point of the second vector to the ending point of the first vector. The resultant is drawn from the starting point of the first vector to the ending point of the second. It is possible to add several different vectors using this method.
The parallelogram method can be used to find the resultant of two vectors that originate at the same point. A parallelogram is a four-sided figure whose opposite sides form parallel lines. A rectangle, for example, is a parallelogram with 90° angles.
The most common of all AC waveforms is the sine wave, because it is produced by a rotating machine. All rotating machines operate on the principle of the sine wave. The pistons in an internal combustion engine, for example, travel up and down inside the cylinder in a sine wave pattern because they are connected to a rotating crankshaft.
Most of the electric power produced in the world is AC. It is used to operate everything from home appliances, such as television sets, computers, microwave ovens, and electric toasters, to the largest motors found in industry. AC has several advantages over DC that make it a better choice for the large-scale production of electric power.
AC voltage can be transformed and DC voltage cannot, which is the main advantage for the use of AC.