Skupovi
Skup čine objekti koji imaju neku zajedničku osobinu i koje na određeni način možemo posmatrati zajedno. Članovi ili objekti koji grade skup zovu se elementi skupa. U matematici se osnovni pojmovi kao što je skup ne definiraju nego se podrazumijevaju jer ih upotrebljavamo za izgradnju drugih matematičkih pojmova.
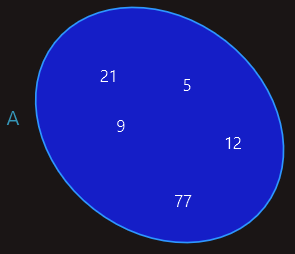
Skupove prikazujemo Vennovim dijagramom i zapisujemo velikim štampanim slovima sa elementima u vitičastim zagradama.
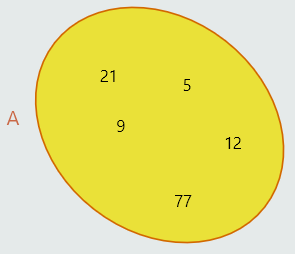
A={5, 9, 12, 21, 77}
Broj 9 pripada skupu A i kažemo da je 9 elemenat skupa A, odnosno 9∈A.
Broj 59 ne pripada skupu A, tako da 59 nije elemenat skupa A i pišemo 59∉A.
Prazan skup označavamo sa ∅ ili {} i kažemo da takav skup nema elemenata.
Broj elemenata nekog skupa nazivamo kardinalni broj i označavamo card (A), pri čemu, naravno, govorimo konkretno o skupu A.
Podskup
A je podskup skupa B ako je svaki elemenat skupa A ujedno i elemenat skupa B, i pišemo A ⊆ B.
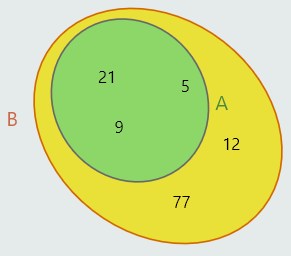
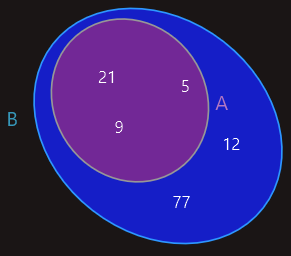
Ako je A podskup skupa B i skup B sadrži barem jedan elemenat koji nije i elemenat skupa A, tada kažemo da je skup A pravi podskup skupa B i pišemo u obliku A ⊂ B.
Za skupove koji sadrže iste elemente kažemo da su jednaki i zapisujemo u obliku A=B.
Unija skupova
Unija skupova A i B je skup A ∪ B koji sadrži sve elemente koji pripadaju barem jednom od skupova A ili B.
A ∪ B = {x∣x∈A ∨ x∈B}
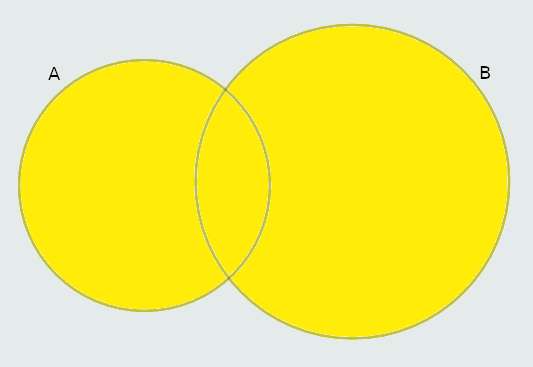
{-5, -4, 7} ∪ {-5, -4, 1} = {-5, -4, 1, 7}
Presjek skupova
Presjek skupova A i B je skup A ∩ B koji sadrži sve elemente koji pripadaju skupu A i skupu B.
A ∩ B = {x∣x∈A ∧ x∈B}
Ako je A ∩ B = ∅, skupovi A i B su disjunktni.
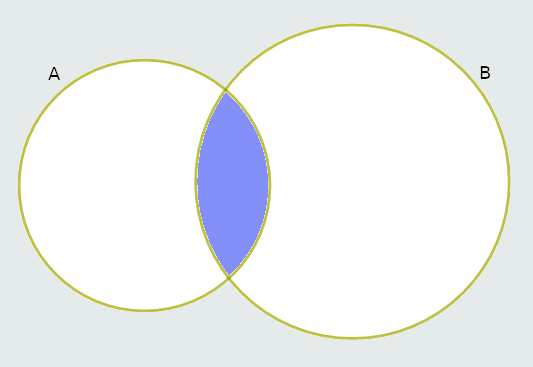
{-11, 5, 7} ∩ {-11, 1, 5} = {-11, 5}
{a, b, c} ∩ {d, e} = ∅
Razlika skupova
Razlika skupova A i B je skup A ∖ B koji sadrži sve elemente koji pripadaju skupu A i koji nisu u skupu B.
A ∖ B = {x∣x∈A ∧ x∉B}
Skup A ∆ B = {A∖B}∪{B∖A} se zove simetrična razlika skupova A i B.

{1, 2, 8} ∖ {0, 4, 5} = {1, 2, 8}
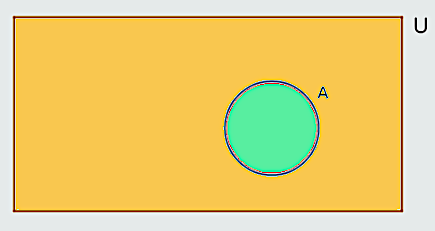
Napomenimo da skup U unutar kojeg posmatramo odnose među njegovim podskupovima nazivamo univerzalni skup. Obično univerzalni skup prikazujemo pravougaonikom, a njegove podskupove elipsama ili krugovima.
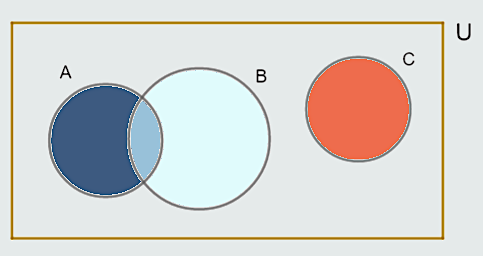
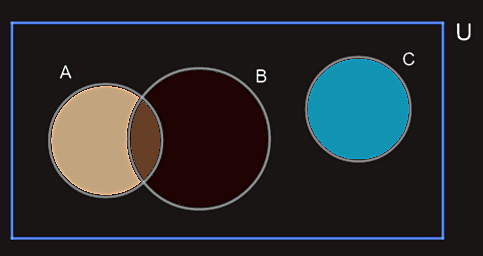
Neka je A ⊆ U. Komplement skupa A je skup svih elemenata univerzalnog skupa U koji nisu u skupu A. Komplement skupa A označavamo A.
A = {x∣x∈U ∧ x∉A}

Skup realnih brojeva
Prirodni brojevi (N)
Sve prirodne brojeve posmatraćemo kao jednu cjelinu, skup koji označavamo slovom N. Ovaj skup ima određena svojstva:
1. nije prazan
2. uređen je
3. skup svih prirodnih brojeva koji su manji od N je konačan
4. skup N nema najvećeg elementa.
Sabiranjem prirodnih brojeva uvijek se dobiva prirodan broj, a isto vrijedi i za množenje.
N = {1, 2, 3, 4, ..........n, n+1, ......}
Vidimo da u skupu prirodnih brojeva postoji prvi element, da je to broj 1 i da za svaki prirodan broj postoji njegov neposredni sljedbenik. Sljedbenik broja 1 je broj 2, sljedbenik broja 2 je broj 3, sljedbenik broja 3 je broj 4, itd. Svaki prirodan broj osim broja 1 ima svog prethodnika.
Kazali smo da operacijama sabiranja i množenja dobivamo novi prirodan broj, npr.:
3+4 = 7
3·4 = 12
Za sabiranje i množenje prirodnih brojeva vrijede određeni zakoni koje uzimamo kao aksiome:
a) zakon komutacije za sabiranje (zakon komutacije za množenje)
b) zakon asocijacije za sabiranje (zakon asocijacije za množenje)
Ove zakone izražavamo na sljedeći način:
1. sabiranje:
a) (∀a∈N, ∀b∈N), a+b=b+a
b) (∀a∈N, ∀b∈N, ∀c∈N), a+(b+c)=(a+b)+c
2. množenje:
a) (∀a∈N, ∀b∈N), a·b=b·a
b) (∀a∈N, ∀b∈N, ∀c∈N), a·(b·c)=(a·b)·c
Operacije sabiranja i množenja prirodnih brojeva vezane su zakonom distribucije množenja u odnosu na sabiranje:
(∀a∈N, ∀b∈N, ∀c∈N), a·(b+c) = a·b+a·c
Skup prirodnih brojeva je uređen skup, što znači da za svaka dva prirodna broja a i b vrijedi jedna od sljedećih relacija:
1. a = b
2. a > b
3. a < b
Za razliku od operacija sabiranja i množenja u skupu N, operacije oduzimanja i dijeljenja u skupu N su uslovne, odnosno nisu definisane za svaka dva prirodna broja. Ako je a>b, tada razlikom brojeva a i b nazivamo broj c=a-b za koji vrijedi b+c=a. Na primjer 9=12-3, jer je 3+9=12. Ovu analogiju možemo primjeniti i na operaciju dijeljenja. Tako je na primjer prirodan broj 12 djeljiv sa brojem 3 jer postoji prirodan broj 4 za koji proizvod 4·3 ima vrijednost 12.
Dakle, u opštem slučaju kažemo da je prirodan broj a djeljiv sa prirodnim brojem b ako postoji prirodan broj c za koji vrijedi da je b·c=a. Ako je prirodan broj a djeljiv sa prirodnim brojem b, pišemo b∣a.
Svaki prirodan broj djeljiv je sa brojem 1 i sa samim sobom.
Zbog djeljivosti prirodnih brojeva, možemo govoriti o prostim i o složenim prirodnim brojevima. Prostim prirodnim brojem nazivamo onaj broj, različit od broja 1, koji je djeljiv sa 1 i sa samim sobom, dok je složeni prirodan broj onaj broj koji je osim sa 1 i sa samim sobom djeljiv sa još nekim, barem jednim prirodnim brojem. Prostih i složenih prirodnih brojeva ima jako mnogo, beskonačno mnogo. Kao što smo kazali da nema najvećeg prirodnog broja, tako nema ni najvećeg prostog niti najvećeg složenog prirodnog broja.
Prosti brojevi su: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,...
Svaki složeni prirodan broj može se prikazati u obliku proizvoda prostih brojeva, tako je na primjer:
18=2·3·3, 42=2·3·7, 102=2·3·17.
Eratostenovo sito naziv je jednostavnog algoritma pomoću kojeg možemo odrediti proste brojeve manje od zadanog broja.
Za skup prirodnih brojeva takođe su vezani i pojmovi paran i neparan broj.
Parnim brojem se naziva onaj prirodan broj koji je djeljiv sa 2, dok je neparan broj onaj koji nije djeljiv sa 2. Svaki paran broj p možemo napisati u obliku: p=2k, k∈N.
Parni brojevi su: 2, 4, 6, 8, 10, 12, 14,..., dok su neparni: 1, 3, 5, 7, 9, 11, 13, 15, 17,...