Prirast funkcije
Ako u opštem slučaju kod funkcije imamo promjenu argumenta x za neki zadani broj, tada možemo označiti broj za koji će se argument mijenjati sa Δx, odnosno novi argument postaje x+Δx.
Promjenu vrijednosti funkcije ili prirast funkcije označit' ćemo sa Δf i računati Δf = f(x+Δx) - f(x).
Graf linearne funkcije
Već smo vidjeli da je graf funkcije skup tačaka T(x,y) gdje se vrijednost ordinate y računa prema zadanom pravilu pridruživanja za sve vrijednosti argumenta x iz domene funkcije f.
Ponekad za ovakav pravac kažemo da ima jednačinu y=ax+b, jer su ordinata y i apscisa x svake njegove tačke povezane pravilom y = f(x) = ax+b.
Graf linearne funkcije f možemo nacrtati ako imamo barem dva para pridruženih vrijednosti (x, f(x)), odnosno potrebne su nam barem dvije tačke u koordinatnom sistemu.
Funkcije čije se vrijednosti povećavaju kad se argument povećava zvat' ćemo rastuće funkcije.
Funkcije čije se vrijednosti smanjuju kad se argument povećava zvat' ćemo padajuće funkcije.
Funkcije koje su ili rastuće ili padajuće su monotone funkcije.
Pravac regresije
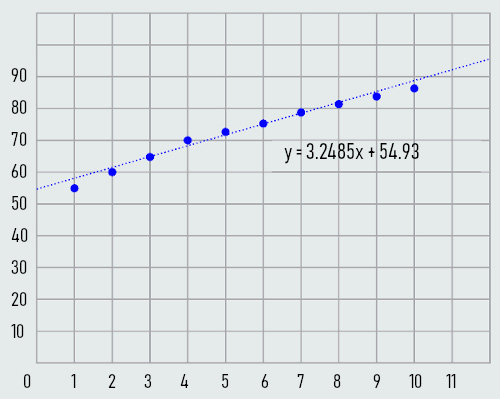
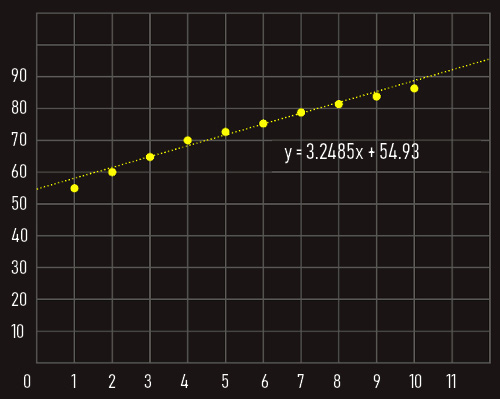
Za gornju sliku kažemo da smo upotrebljavali linearnu regresiju, a dobiveni pravac zovemo pravac regresije.
Pravac regresije je pravac koji najbolje povezuje, odnosno aproksimira zadane tačke grafa, koje bez ovog pravca predstavljaju tzv. dijagram rasipanja; na konkretnom primjeru je primjetan porast s vremenom (y=f(x), dobiveni dijagram je funkcija vremena y=f(t)).
Postoje razni kriteriji po kojima se određuje koji pravac najbolje aproksimira zadane tačke. Jedan od najčešćih je tzv. metoda najmanjih kvadrata. Ideja metode je da se minimizira zbir kvadratnih odstupanja eksperimentalnih y vrijednosti (dobivenih podataka - tačaka) od teoretskih yt (pravac). Onaj pravac za koji je zbir kvadrata udaljenosti (y−yt)2 svih tačaka od pravca najmanji je pravac regresije.
Neke skupove podataka možemo bolje, a neke lošije opisati linearnom funkcijom. Linearnu povezanost mjerimo Pearsonovim koeficijentom korelacije (r), -1 ≤ r ≤ 1. Što je vrijednost koeficijenta korelacije bliže broju 1 ili −1,povezanost je bolja. Ako je r=0, nema povezanosti.
Polinomi i racionalne funkcije
Polinomi su najjednostavniji i ujedno najvažniji primjeri funkcija; možemo ih sabirati, oduzimati i množiti - rezultat je uvijek polinom. Najstariji koeficijent polinoma je broj koji dolazi uz najveću potenciju varijable x; kada potencije varijable x opadaju u napisanom obliku polinoma, kažemo da je polinom u sređenom obliku.
Na primjer, ako imamo zadate polinome f(x) = 2x-5 i g(x) = x2+x-1, njihov zbir h = f+g je novi polinom:
h(x) = (2x-5) + (x2+x-1) = x2+3x-6
Oduzimanje polinoma radimo na identičan način.
Ako je c≠0 bilo koji realan broj, onda funkciju f: R → R za koju je f(x) = c, za svako x∈R, nazivamo polinom nultog stepena. Npr. f(x) = -6.
U slučaju da je f(x) = 0, takvu funkciju zovemo nulfunkcija ili nulpolinom.
Teorema: Proizvod polinoma f i g je polinom f·g, a dobiva se tako da se svaki član polinoma f množi sa svakim članom polinoma g i dobiveni proizvodi saberu. Stepen proizvoda polinoma jednak je zbiru stepeni polinoma koji se množe.
f1(x) = a1x + a0 (a1≠0), polinom prvog stepena
f2(x) = a2x2 + a1x + a0 (a2≠0), polinom drugog stepena
f3(x) = a3x3 + a2x2 + a1x + a0 (a3≠0), polinom trećeg stepena
Polinom n-tog stepena je funkcija sa R u R oblika:
fn(x) = anxn + an-1xn-1 + ... + a1x + a0 (an≠0),
gdje su a0, a1, ... an dati realni brojevi, koeficijenti polinoma fn, pri čemu se pretpostavlja da je najstariji koeficijent an ≠ 0.
Suprotni polinom polinoma f je polinom g takav da je f+g = 0 i taj polinom označavamo sa -f.
Napomena: Ovdje sada nećemo obrađivati dijeljenje polinoma...
Racionalne funkcije
Racionalne funkcije definišemo pomoću polinoma na sličan način kao što se racionalni brojevi definišu pomoću cijelih brojeva, te se s racionalnim funkcijama računa na sličan način kao sa racionalnim brojevima, pri čemu je i rezultat (zbir, razlika, proizvod, količnik) ponovo racionalna funkcija.
Racionalna funkcija, općenito, ima oblik:
f(x) = A(x)/B(x), pri čemu su A i B polinomi i pretpostavlja se da B nije nulpolinom.
Na primjer, f(x) = [x2-x+1]/[x-2] predstavlja racionalnu funkciju, itd.
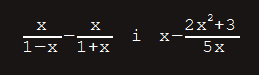
Zadatak: Pomnožimo racionalne funkcije: 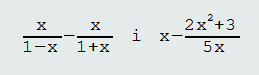
Rješenje:
Potrebno je doći do rješenja f(x) = -(6⁄5)x
Ako su A i B polinomi, onda se domena D(f) funkcije f(x) = A(x)/B(x) [racionalna funkcija] sastoji od onih realnih brojeva x za koje je B(x) ≠ 0; → D(f) = {x ∈ R: B(x) ≠ 0}.
Stepeni i korijeni
Za realan broj a i prirodne brojeve m i n, vrijede formule:
am·an = a(m+n),
am/an = a(m-n).
Takođe vrijedi:
a-n = 1/an, a0 = 1 (prema definiciji) ⇒ a0/an = a(0-n) = a-n
Teorema: Ako je a≠0 realan broj, onda vrijedi:
(am)n = am·n za sve cijele brojeve m i n.
Tako je npr. (a2)3 = a2 · a2 · a2 = a2+2+2 = a2·3 = a6.