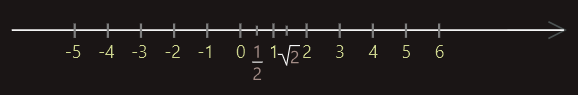Realni brojevi (R=QUI)
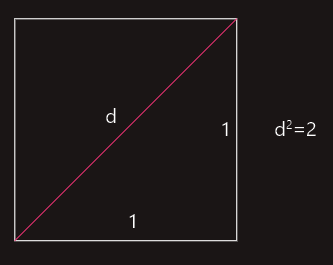
Realni brojevi su svi racionalni i svi iracionalni brojevi. Iracionalni brojevi se mogu napisati u decimalnom razvoju, ali se pri tome dobivaju beskonačni neperiodični decimalni brojevi. Tako je na primjer, iracionalan broj broj čiji je kvadrat jednak broju 2.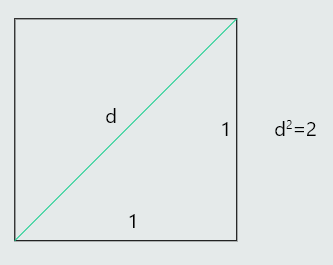
Takođe, govoreći o skupovima brojeva, vrijedi: N⊂N0⊂Z⊂Q⊂R.
Svi realni brojevi mogu se prikazati na jednoj pravoj koju zovemo brojna osa. Svakoj tački prave pridružujemo jedan broj.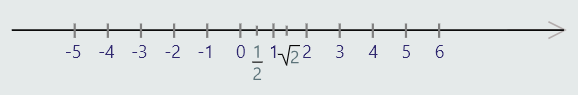
Jasno je da je udaljenost nekog broja od početka (0) jednaka i sa lijeve i sa desne strane, i zapravo predstavlja apsolutnu vrijednost tog broja, npr. -5 = 5.
Prava i ravan
Osim skupova N, Z, Q i R postoje i skupovi prava i ravan, čije elemente nazivamo tačkama.
Kroz dvije tačke prolazi prava i to samo jedna prava; kažemo da je prava određena dvjema tačkama. Ako tačke A i B leže u ravni M, tada i prava p određena tim dvjema tačkama leži u ravni M. Tačkama A i B prave p određena je duž AB, što je skup svih tačaka T prave p koje leže između tačaka A i B. I tačke A i B pripadaju duži AB i zovemo ih krajnje tačke. Duž CD je dio duži AB, pri čemu je CD podskup skupa AB i kažemo da je duž CD manja od duži AB, odnosno duž AB je veća od duži CD. 
Kao što se do prirodnih brojeva došlo zbog potrebe za brojanjem (prebrojavanjem), tako se i do racionalnih, pa i realnih brojeva došlo zbog potrebe za mjerenjem. Jedinica za mjerenje dužine je metar. U Sevresu kod Pariza, u Međunarodnom uredu za mjere i utege, čuva se određena, specijalno izrađena metalna motka dužine 1 metar.
U gornjem primjeru smo kazali da je AB neka proizvoljna duž. Sada ćemo od ishodišta O na koordinatnoj osi nanijeti duž AB i dobiti tačku D takvu da je njezina koordinata d pozitivan realan broj. 
Tako dobiven broj d zovemo dužina duži AB, odnosno udaljenost tačaka A i B, koji označavamo sa AB ili d(A, B).
Pitagorina teorema
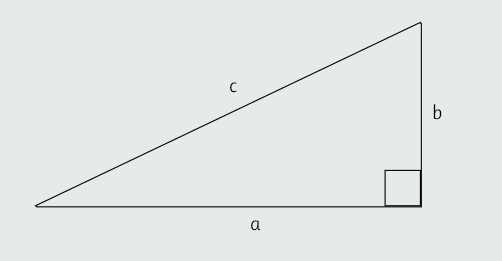
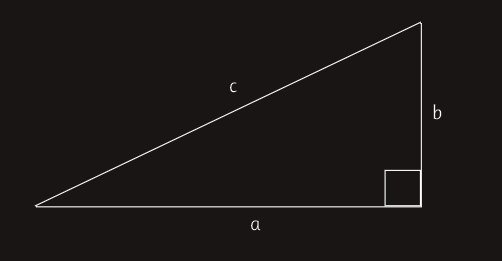
Ako su a i b dužine kateta i c dužina hipotenuze pravouglog trougla, onda je a2+b2=c2.
Ako je a=b=1, tada je c2=2, pa c nije racionalan broj. Ovdje se radi, dakle, o dijagonali kvadrata.
Kvadrat kojem je stranica jedinična duž zove se jedinični kvadrat i on je jedinica za mjerenje površine, dok je kocka kojoj je ivica jedinična duž - jedinična kocka i ona je jedinica za mjerenje zapremine.
Funkcije
Ako je svakom elementu x skupa S pridružen po jedan element y skupa S', onda kažemo da je zadata funkcija f sa skupa S u skup S'.
Skup S zovemo domena (područje definicije), a skup S' kodomena funkcije f.
Pišemo f:S->S', odnosno f djeluje sa S u S'.
Na slici ispod je naznačeno da funkcija f element x iz skupa S prevodi u element y iz skupa S' i pišemo u obliku x->f(x).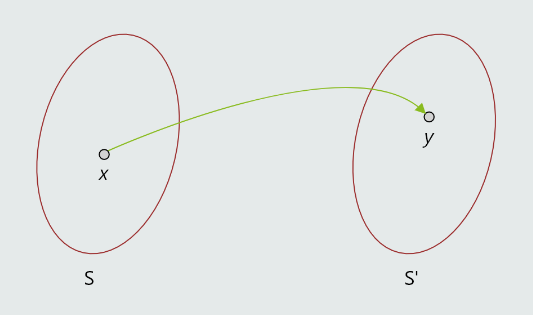 
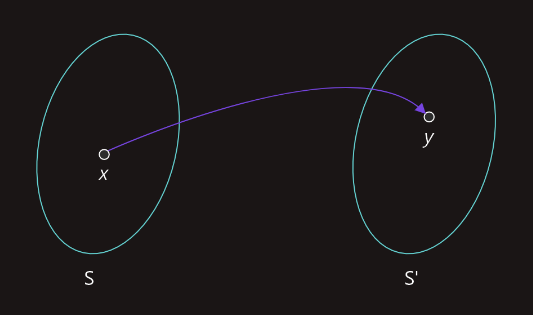
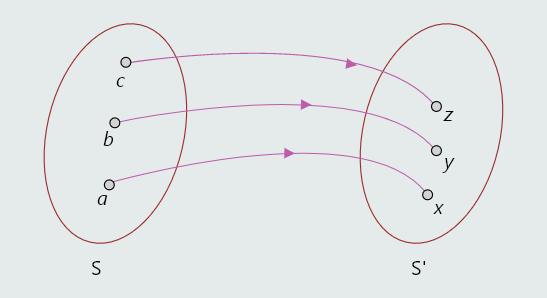
Vidimo da je svakom elementu x∈S pridružen tačno jedan element y∈S', tako da pišemo y=f(x) i kažemo da je y slika od x.
Na sljedećoj slici iz elementa x∈S izlaze dvije strelice koje završavaju u skupu S', tako da ovakav slučaj ne predstavlja funkciju.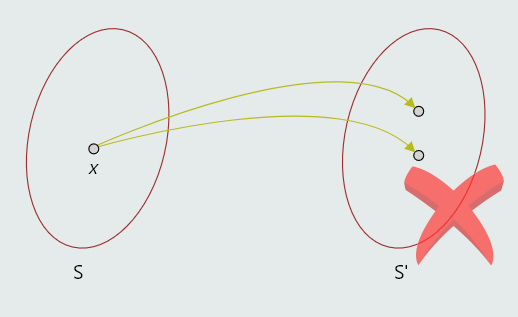 
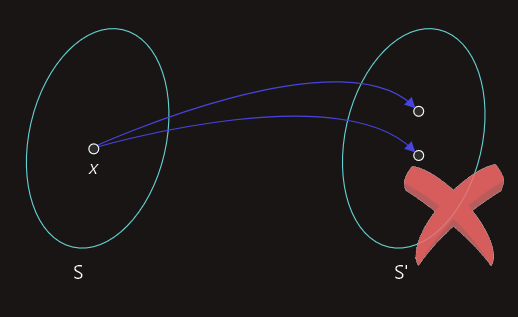
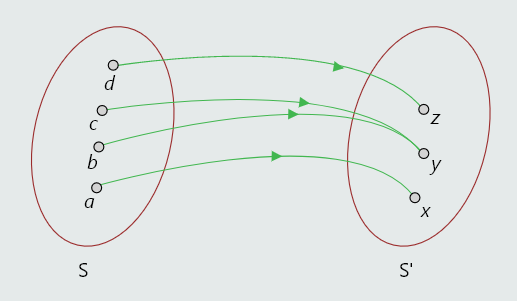
Obrnuto se može dogoditi, što je predstavljeno na sljedećoj slici:
Vidimo da je f(b)=y i f(c)=y.
Funkcija za koju se to nikad ne dogodi zove se injekcija ili injektivno preslikavanje.
Funkcija f:S->S' je injekcija ako ona različite elemente skupa S preslikava u različite elemente skupa S', odnosno kada je x1≠x2 onda je f(x1)≠f(x2).
Funkcija f:S->S' je surjekcija sa S na S' ako za svaki elemenat y∈S' postoji bar jedan elemenat x∈S takav da je f(x)=y.
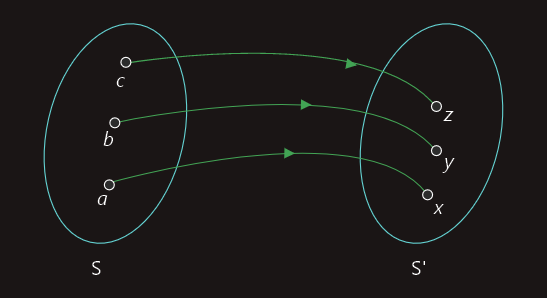
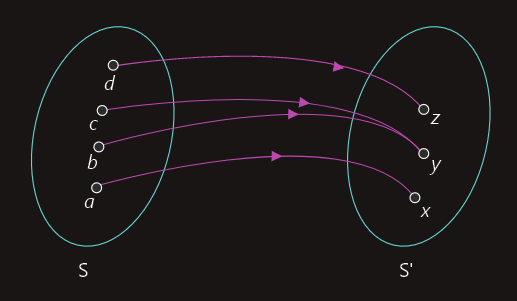
Funkcija f:S->S' je bijekcija (obostrano jednoznačno preslikavanje) ako je f injekcija i surjekcija.
Na gornjoj slici funkcija je surjekcija, ali nije injekcija, tako da nije ni bijekcija. Slika ispod prikazuje bijekciju. 
