Omjeri, razmjeri, postotci, aritmetička sredina
Omjeri
Odnos dviju količina ili mjera a i b u datoj situaciji nazivamo omjerom i zapisujemo u obliku a:b.
a:b=a⁄b, (a,b)∈R, b≠0
Na slici su prikazana dva skupa, A i B.
Promatramo li apsolutne odnose, reći ćemo da skup A sadrži jednak broj krugova kao skup B. Međutim, ako promatramo relativne odnose, reći ćemo da skup A sadrži više krugova od skupa B.
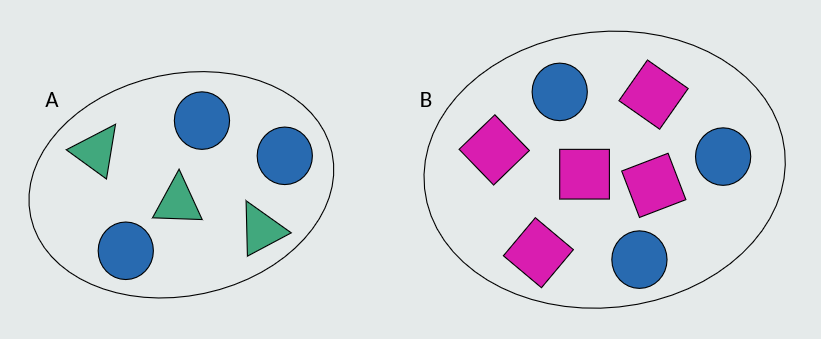
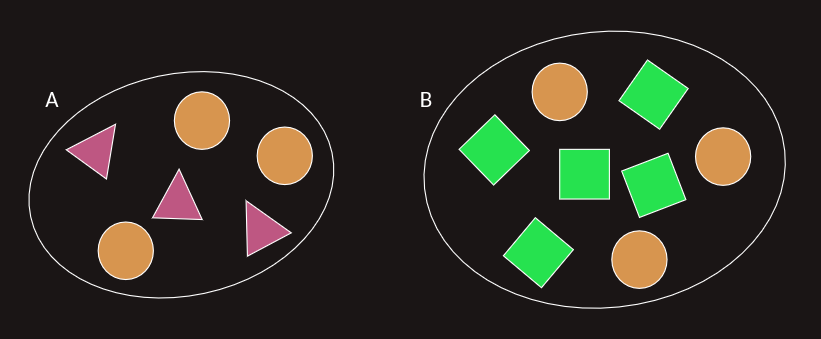
Skup A sadrži 6 elemenata od kojih su 3 kruga. Skup B sadrži 8 elemenata od kojih su takođe 3 kruga. Odnos broja krugova prema ukupnom broju elemenata skupa A iznosi 3:6, a odnos broja krugova prema broju elemenata skupa B iznosi 3:8.
Vidimo da je taj broj za skup A veći pa kažemo da skup A sadrži više krugova.
Produženi omjer je kraći zapis više omjera u kojem je drugi član svakog omjera jednak prvom članu sljedećeg omjera.
Ako imamo omjere a:b i b:c, onda ih možemo zapisati u obliku produženog omjera, tj. a:b:c.
Razmjeri
Jednakost omjera a:b=c:d, (a,b,c,d)∈R, b,d≠0 nazivamo razmjerom.
Kažemo da su dvije veličine a i b u zlatnom omjeru ili zlatnom rezu ako se manji dio a odnosi prema većem b kao što se veći dio odnosi prema ukupnom, odnosno ako vrijedi a:b=b:(a+b).
Postotci
Postotak je razlomak s nazivnikom 100.
p % = p⁄100
Postotak označava koliko jedinica jedne veličine dolazi na 100 jedinica iste veličine.
U kvadratu 10x10 sa slike koliko je kvadratića obojeno drugom bojom?
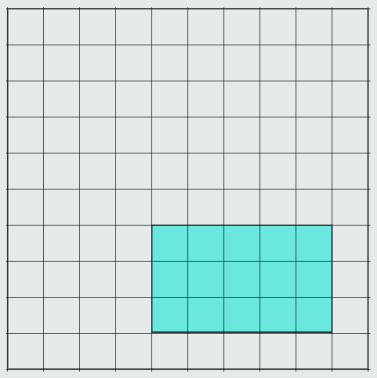
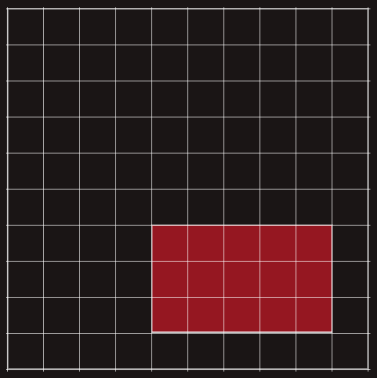
Vidimo da je od 100 kvadratića početne mreže, ukupno obojeno njih 15, dakle imamo postotak 15⁄100, odnosno 15% površine početnog kvadrata.
Promil označava koliko jedinica jedne veličine dolazi na 1000 jedinica iste veličine, odnosno promil je razlomak s nazivnikom 1000, p ‰ = p⁄1000.
Aritmetička sredina
Aritmetička sredina ili prosjek x za neki konačan skup brojeva S={x1, x2, x3, ... xn} računa se kao količnik zbira članova tog skupa i broja članova tog skupa, odnosno:
x=(x1+x2+x3+...+xn)⁄n
Algebarski izrazi
Stepeni
Stepeni sa prirodnim eksponentom
Za bilo koji realan broj a i bilo koji prirodan broj n vrijedi da je an=a·a·a·...·a (n faktora).
Broj a nazivamo baza a broj n eksponent stepena.
Množenje stepena jednakih baza izvodi se na sljedeći način: am·an=am+n.
Zaista je npr. a2·a3=(a·a)·(a·a·a)=a5.
Dalje, vrijedi da je (a·b)n=an·bn.
Tako je npr. (2·3)3=23·33=63=216
Odnosno, imamo da je (2·3)·(2·3)·(2·3)=2·2·2·3·3·3=8·27=216
Takođe je (a⁄b)n=an⁄bn.
Stepene jednakih baza dijelimo na način da je am:an=am-n (a≠0, m>n).
Stepen se može stepenovati pri čemu važi da je (am)n=am·n.
Stepeni sa cijelim eksponentom
Vidjeli smo u gornjem uslovu da je dijeljenje stepena jednakih baza sa prirodnim eksponentom definisano za a≠0 i m>n.
Ako se radi o slučaju da je m=n, tada bismo imali an:an=1, kao količnik dva jednaka broja.
Dakle, po definiciji uzimamo da je a0=1, jer je a0=an:an=an-n (a≠0).
Razmotrimo sada situaciju da je m<n.
Tada postoji prirodan broj k takav da je m+k=n, odnosno m-n=-k.
Sada imamo am:an=am-n=a-k.
Kako je a-k ustvari jednako a0-k=a0:ak, to je dalje jednako 1⁄ak, pri čemu je a≠0.
Za ostale operacije sa stepenima čiji je eksponent cijeli broj vrijede ista pravila kao i u slučaju da je prirodan broj.
Cijeli algebarski izrazi
Izraz je bilo koji konačan broj konstanti i promjenljivih koje su povezane znacima operacija (sabiranja, množenja, oduzimanja, dijeljenja, stepenovanja...).
Konstanta je jedinstvena i potpuno određena vrijednost, npr. 1, -3⁄4, 128 ...
Promjenljiva (varijabla) je vrijednost x koja "uzima" vrijednost iz skupa R ili nekog njegovog podskupa. Ako npr. kažemo da x∈{-4, 0, 7, 22, 30}, tada x može biti bilo koja od pet vrijednosti iz skupa i onda x predstavlja promjenljivu ili varijablu. Promjenljive označavamo slovima a, b, c, ... x, y, z.
Dakle, izrazi su npr. (a+6), 12-(x+4)2, x+2·y ...
Algebarski izraz je takav izraz koji je sastavljen od konstanti i promjenljivih koje su povezane znacima operacija sabiranja, oduzimanja, množenja, dijeljenja, stepenovanja sa cijelim eksponentom i korjenovanja.
Racionalni algebarski izraz je izraz koji ne sadrži korijene.
Racionalni algebarski izraz je cijeli algebarski izraz ako ne sadrži dijeljenje izrazima koji sadrže varijable.
Na primjer: (x2-4x):(x+2) nije cijeli algebarski izraz.
Kada imamo izraz bez varijabli, onda se izvršavanjem naznačenih operacija u izrazu dobije određeni broj koji zovemo vrijednost izraza.
Ako se, međutim, u izrazu nalaze i varijable, tada za različite vrijednosti varijabli dobivamo i različite vrijednosti izraza.
Polinomi jedne promjenljive
Monomi
Algebarski izrazi u kojima su konstante i promjenljive povezane samo znacima operacija množenja i stepenovanja nazivaju se monomi.
Navedimo nekoliko monoma: 16, 5x, 22a2b, -28 ...
Konstanta u monomu se zove koeficijent, a ostali dio je glavna veličina monoma.
Kod monoma 5x2y3 koeficijent je 5, a glavni dio je x2y3.
Za monome kažemo da su slični ako su im glavne veličine potpuno jednake.
Slični monomi se mogu sabirati i oduzimati, dok se svi monomi mogu množiti.
Pogledajmo dva primjera:
1. 5x2y3-3x2y3+11x2y3=(5-3+11)x2y3=13x2y3
2. -4x3y4·5a2xy2=(-4·5)·(x3y4·a2xy2)=-20a2x4y6
Polinomi
Zbir dva ili više monoma čini cijeli algebarski izraz koji nazivamo polinom, pri čemu su monomi sada članovi polinoma.
Na primjer: 2a2b3+4ax2-11ab5.
Polinom od dva člana zovemo binom, a od tri člana trinom.