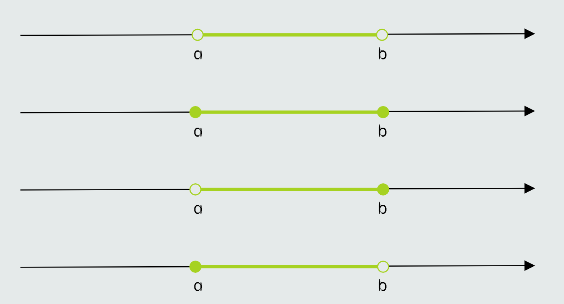
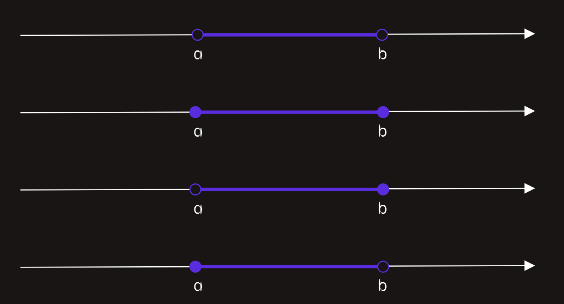


Intervali su skupovi tako da je moguće odrediti uniju, presjek i razliku intervala.
Presjek skupova A i B čine elementi koji se nalaze i u skupu A i u skupu B.
Primjer:
Odredimo presjek intervala [3,5] i [2,4): 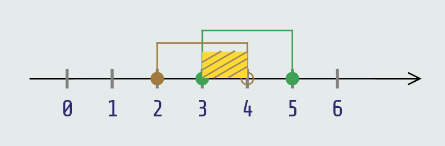
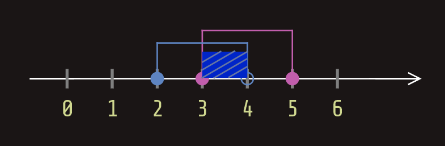
Uniju skupova A i B čine elementi koji se nalaze u skupu A ili u skupu B.
Primjer:
Odredimo uniju intervala [3,5] i [2,4): 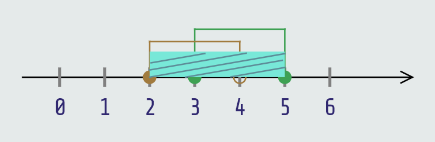
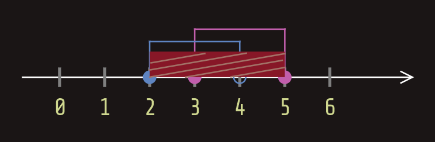
Primjer:
Odredimo za intervale (4, ∞) i [-2, 1] presjek i uniju.
U ovom slučaju, ova dva intervala nemaju zajedničkih tačaka tako da je njihov presjek prazan skup, dok se unija sastoji od dvaju nepovezanih dijelova pa je možemo napisati u obliku jednog intervala: [-2, 1] ∪ (4, ∞).
Rješavanje linearnih nejednačina
Rješenje linearne nejednačine može biti:
1. interval realnih brojeva
2. skup svih realnih brojeva
3. nema rješenja
Ako prilikom rješavanja linearne nejednačine dobijemo nejednakost koja nije istinita, onda nejednačina nema rješenja.
U slučaju da nejednakost uvijek vrijedi, tada je rješenje nejednačine skup svih realnih brojeva.
Zadatak:
Pronađimo rješenje nejednačine: 2x+7 < 3-5x
Rješenje:
2x+7 < 3-5x
2x+5x < 3-7
7x < -4
x < -4⁄7
Dakle, rješenje nejednačine je skup (-∞, -4⁄7) 
Rješavanje sistema nejednačina
Sistem dvije linearne nejednačine
Sistem dvije linearne nejednačine s jednom nepoznatom sastoji se od dviju linearnih nejednačina; riješiti ovakav sistem znači odrediti skup svih realnih brojeva koji su rješenja prve i druge nejednačine.
Na primjer, rješenje nejednačine 3x+230 ≤ 500 je x ≤ 90, pa je rješenje svaki realan broj iz intervala (-∞, 90], a rješenje nejednačine 2x+60 > 200 je x > 70, pa je rješenje svaki realan broj iz intervala (70, ∞).
Ovdje tražimo skup brojeva koji pripadaju i prvom i drugom intervalu, odnosno tražimo presjek ova dva intervala.
Možemo presjek ova dva intervala i skicirati, kako smo to ranije radili i dobili bismo zajedničko rješenje dviju nejednačina: (70, 90].
Sistem triju linearnih nejednačina
Sistem s više od dvije nejednačine rješavamo na isti način, tj. tražimo realne brojeve koji zadovoljavaju rješenja svih nejednačina. Ovo znači da trebamo odrediti presjek skupova rješenja svake pojedinačne nejednačine u sistemu.
Ako na primjer imamo sistem nejednačina:
4x-3 > 5
10-2x ≥ 2
5+3x > 14
------------
Rješenja pojedinačnih nejednačina su:
x > 2
x ≤ 4
x > 3
------------------------------------
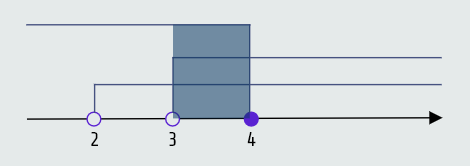
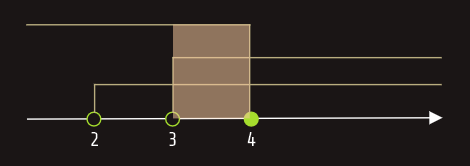
Skup rješenja je (3, 4].
Ako je zadana nejednačina (x+5)(x-4) < 0, množenjem zagrada dobili bismo nelinearnu nejednačinu x2+x-20 < 0, ali datu nejednačinu možemo riješiti na drugačiji način.
Moguća su dva slučaja da bi (x+5)(x-4) bilo < 0:
1. x+5 > 0 i x-4 < 0 ili
2. x+5 < 0 i x-4 > 0
--------------------------------------
Skup rješenja u prvom slučaju je presjek intervala (-5, ∞) i (-∞, 4), pa je skup rješenja (-5, 4).
U drugom slučaju, skup rješenja je presjek intervala (-∞, -5) i (4, ∞), tako da je skup rješenja prazan skup.
Na kraju, potrebno je napraviti uniju ova dva skupa rješenja da bismo dobili konačno rješenje: (-5, 4) ∪ 0 = (-5, 4).
Nejednačinu oblika (x/(x-1)) ≤ 3, napisat' ćemo tako da na jednoj strani ostane nula.
(x/(x-1))-3 ≤ 0
((x-3x+3)/(x-1)) ≤ 0
((-2x+3)/(x-1)) ≤ 0
----------------------
Ovdje imamo dva slučaja, pri čemu treba paziti da nazivnik ne smije biti jednak 0.
1. -2x+3 ≤ 0 i x-1 > 0 ili
2. -2x+3 ≥ 0 i x-1 < 0
---------------------------------------------------------------------------------
Rješenje u prvom slučaju je: [3⁄2, ∞).
Rješenje u drugom slučaju je: (-∞, 1).
Konačno rješenje je: (-∞, 1) ∪ [3⁄2, ∞).
Nejednačine s apsolutnim vrijednostima
x ≤ a, a∈R
1. a < 0 ------> NEMA RJEŠENJA
2. a = 0 ------> POSTOJI JEDNO RJEŠENJE x=0
3. a > 0 ------> RJEŠENJE JE: -a ≤ x ≤ a <=> x ∈ [-a, a]
x ≥ a, a∈R
1. a ≤ 0 ------> RJEŠENJE JE: svi realni brojevi x
2. a > 0 ------> RJEŠENJE ZAPISUJEMO: x ≤ -a ili x ≥ a <=> x ∈ (-∞, -a] ∪ [a, ∞)


Zadatak:
Potrebno je riješiti nejednačinu: 1 ≤ x < 7
Rješenje:
1. x ≥ 1
x ∈ (-∞, -1] ∪ [1, ∞) i:
2. x < 7
x ∈ (-7, 7)
Konačno rješenje je presjek dobivenih skupova.
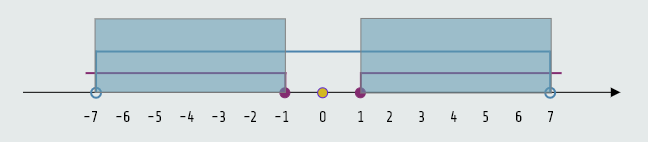
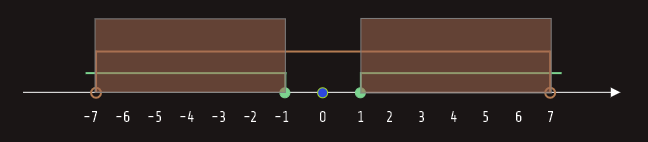
Nakon skiciranja na brojnoj osi, rješenje zadate nejednačine je unija intervala (-7, -1] ∪ [1, 7).