Uređaj na skupu realnih brojeva
Linearna algebarska jednačina prvog stepena

Prolaznik brdskim krajem primjeti veliko stado ovaca, zaustavi se pored čobanina i pita ga koliko ima ovaca.
Čobanin, nakon kratkog razmišljanja odgovori: "Moj brat ima 80 ovaca; da je moje stado tri puta brojnije, zajedno bismo imali 245 ovaca."
Prolaznik se zamisli, uze papir i olovku i napisa:
3x+80=245
Dakle, problem iskazan riječima predstavljen je pomoću matematičkog modela, odnosno data je jednačina iz koje treba odrediti nepoznatu x.
Gornju jednačinu rješavamo na način:
3x=245-80
3x=165
x=55
Provjerom ćemo dobiti da je 3·55+80 zaista jednako 245.
Jednačina oblika ax=b zove se linearna algebarska jednačina prvog stepena sa jednom nepoznatom.
Teorema
Jednačina ax=b ima:
1. jedinstveno rješenje x=b/a ako je a≠0
2. beskonačno rješenja ako je a=0 i b=0 (svaki realan broj je rješenje jednačine)
3. nema nijednog rješenja ako je a=0 i b≠0
Dvije ili više jednačina su ekvivalentne ako imaju isti skup rješenja.
Važe sljedeća pravila:
1. ako svakoj strani jednačine dodamo isti broj, ona prelazi u ekvivalentnu jednačinu
2. ako svakoj strani jednačine oduzmemo isti broj, ona prelazi u ekvivalentnu jednačinu
3. ako svaku stranu jednačine pomnožimo istim brojem, koji je različit od nule, ona prelazi u ekvivalentnu jednačinu
4. ako svaku stranu jednačine podijelimo istim brojem, koji je različit od nule, ona prelazi u ekvivalentnu jednačinu
5. ako s jedne strane jednačine prenesemo broj na drugu stranu, ali tako da taj broj promjeni predznak, jednačina prelazi u ekvivalentnu jednačinu
6. faktor se dijeljenjem može prebaciti na drugu stranu jednačine, s tim da on postane divizor (λ≠0 prelazi u 1/λ) i jednačina prelazi u ekvivalentnu jednačinu
Jednačine koje se svode na linearne jednačine
Primjetit' ćemo da neke jednačine izgledaju složeno, ali ih jednostavnim računskim radnjama možemo svesti na linearne. Važno je istaći da za jednačine kojima je nepoznata u nazivniku treba nakon rješavanja provjeriti da li prihvatamo rješenje ili ne.
Riješimo na primjer jednačinu: (x+2)⁄(x2-4)=0
Ova se jednačina svodi na linearnu jer znamo da je razlomak jednak nuli ako mu je brojnik jednak nuli, tj.
x+2=0
x=-2
Međutim, provjerom ćemo utvrditi da kada ovo rješenje uvrstimo u zadani razlomak, odnosno u nazivnik razlomka, imamo da je nazivnik jednak nuli ((-2)2-4)=(4-4)=0, što znači da ova jednačina nema rješenja.
Jednačine s apsolutnim vrijednostima
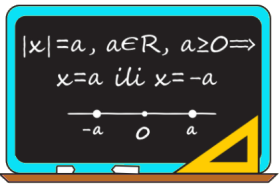
Osnovna jednačina s apsolutnom vrijednosti je jednačina oblika x=a, a∈R, a≥0.
U geometrijskom smislu, x su brojevi koji su na brojnoj osi od 0 udaljeni za a.
Rješenje gornje jednačine je:
• x=a ili x=-a ako je a>0
• 0 ako je a=0
• nema rješenja ako je a<0
Zadatak:
Pronađimo rješenje jednačine 2x-3=3x.
Rješenje:
Uslov da jednačina ima rješenje je 3x≥0. Na kraju ćemo provjeriti da li je uslov ispunjen za dobivena rješenja.
2x-3=-3x
2x+3x=3
5x=3
x=3⁄5
ili 2x-3=3x
2x-3x=3
-x=3
x=-3
S obzirom da mora biti 3x≥0, jedino zadovoljavajuće rješenje je x=3⁄5.
x=y <=> x=y ili x=-y
Svojstva uređaja na skupu realnih brojeva
Realne brojeve možemo prikazati na brojnoj pravoj; realni broj može biti pozitivan, negativan ili nula. 

Ako je realni broj a pozitivan, pišemo a>0; odnosno za negativan realni broj a pišemo a<0.
Ovdje smo uporedili broj a sa nulom, na isti način možemo uporediti dva realna broja a i b.
Ako je a na brojnoj pravoj desno od broja b, kažemo da je a veći od b i zapisujemo a>b; ako je a na brojnoj pravoj lijevo od broja b, kažemo da je a manji od b i zapisujemo a<b.
Prethodno je opisano kako realne brojeve možemo upoređivati po veličini pa kažemo da smo u skup realnih brojeva uveli uređaj.
Svojstva
Za bilo koja dva realna broja x i y vrijedi samo jedna od tri mogućnosti:
x<y ili x>y ili x=y (tzv. zakon trihotomije)
Zatim, ako je a<b i b<c, tada je a<c.
(a<b i b<c) ⇒ a<c (tranzitivnost uređaja)
U ovom slučaju možemo pisati produženu nejednakost: a<b<c ili c>b>a.
Za a≤b kažemo da je a manje ili jednako od b, a za a≥b kažemo da je a veće ili jednako od b.
Za svaki realan broj x i ako je a<b vrijedi:
(a<b) ⇒ (a+x<b+x) (monotonost sabiranja)
Nejednakost ne mijenja smisao ako lijevoj i desnoj strani te nejednakosti dodamo isti broj.
Množenje nejednakosti a<b pozitivnim brojem p ne mijenja smisao nejednakosti.
(a<b i p>0) ⇒ (a·p<b·p) (monotonost množenja)
Ako broj prebacimo s jedne strane nejednakosti na drugu stranu, nejednakost ne mijenja smisao a broj koji prebacujemo mijenja predznak.
Množenje nejednakosti negativnim brojem mijenja smisao nejednakosti.
Na primjer:
4<7 i ako pomnožimo nejednakost brojem -3 vrijedi:
4·(-3)>7·(-3), odnosno (-12)>(-21)
Kvadrat realnog broja različitog od nule je pozitivan broj.
(x≠0) ⇒ (x2>0)
Na osnovu navedenih osnovnih svojstava uređaja na skupu R lako je izvesti i mnoga druga svojstva.
Intervali
Intervali su podskupovi skupa realnih brojeva zadani nejednakostima.
Na sljedećoj slici su prikazani:
1. otvoreni interval (a,b)={x∈R: x>a i x<b}
2. zatvoreni interval [a,b]={x∈R: x≥a i x≤b}
3. poluotvoreni ili poluzatvoreni interval (a,b]={x∈R: x>a i x≤b} [a,b)={x∈R: x≥a i x<b}