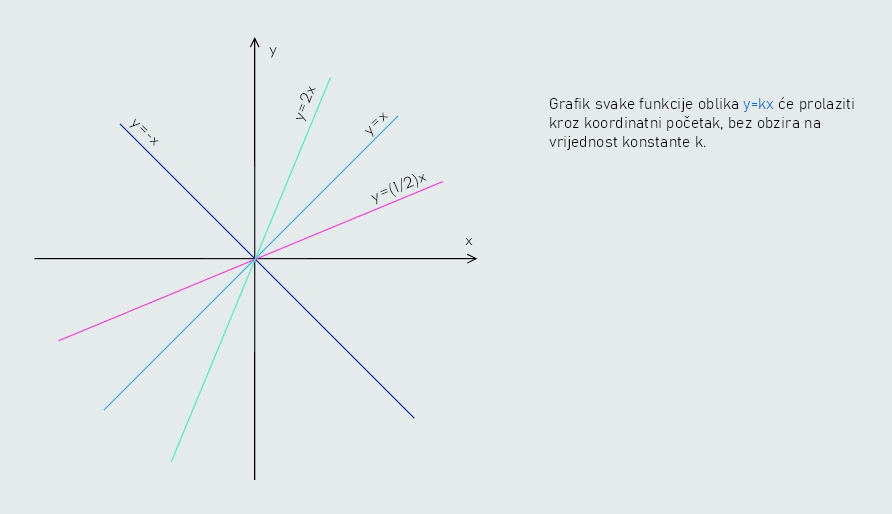
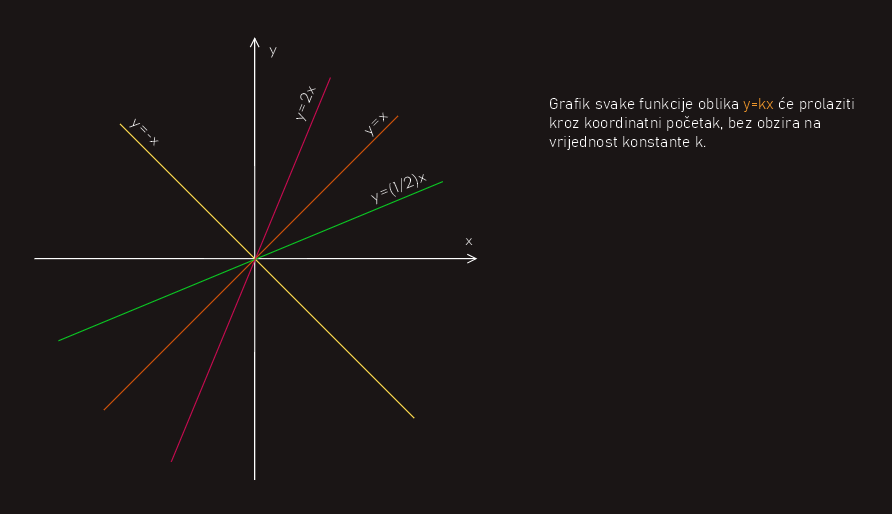
Jedna vrijednost varijable x i odgovarajuća vrijednost varijable y određuju jednu tačku. Određivanjem takvih tačaka možemo funkciju grafički prikazati. Dakle, na gornjoj slici su prikazani grafovi funkcije za nekoliko vrijednosti koeficijenta k. Vidimo da znak konstante koja se naziva koeficijent proporcionalnosti utiče na položaj prave u koordinatnom sistemu.
Takođe, funkcija y=f(x) raste ako za x1<x2 ⇒ y1<y2, a opada ako za x1<x2 ⇒ y1>y2.
Za funkciju y=f(x) postoje dva bitno različita slučaja:
1. k>0
2. k<0
Na osnovu ovih slučajeva možemo pratiti promjene i znati tok funkcije, tj. kada funkcija raste, kada opada...
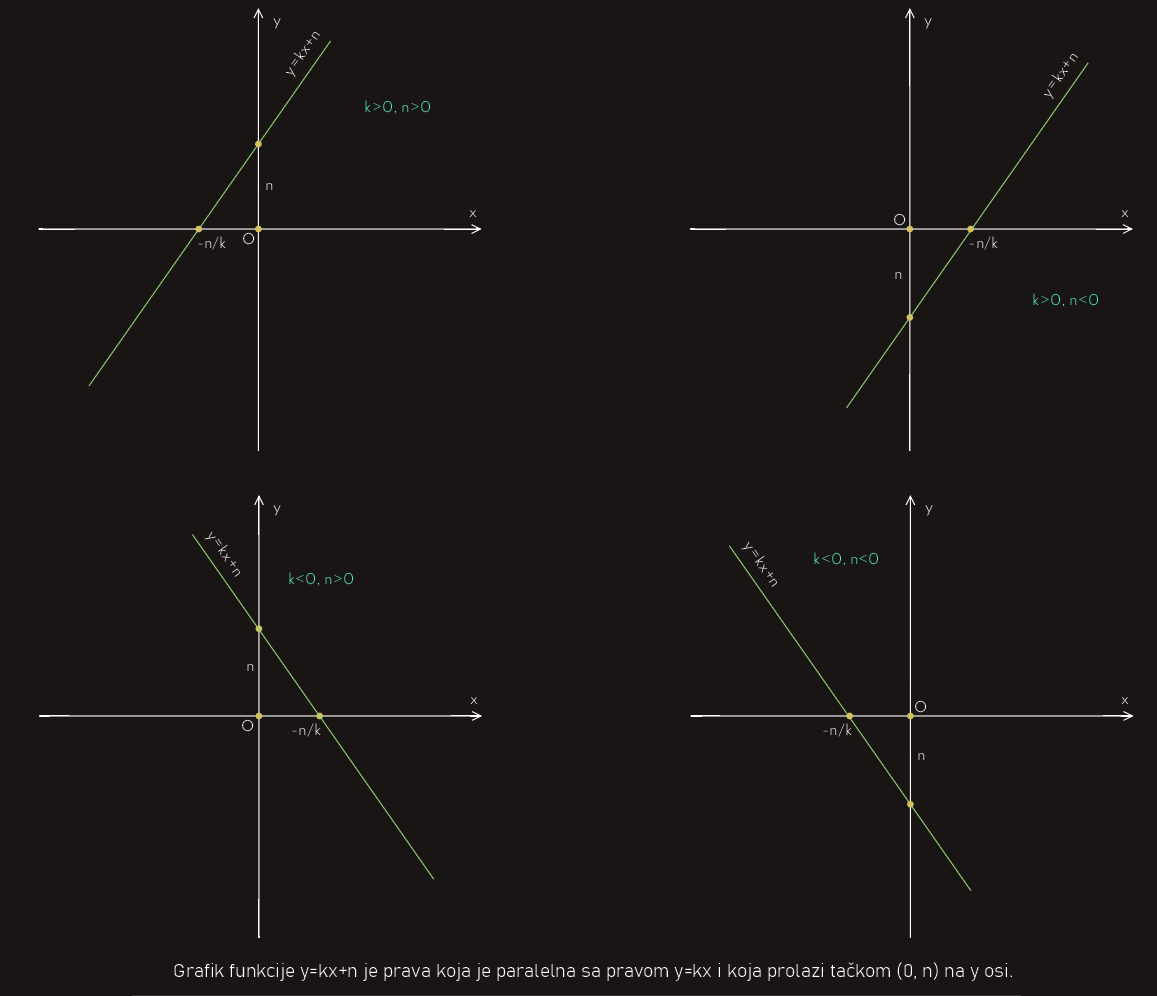
Grafik linearne funkcije je prava linija. Kako se pruža ta linija funkcije zavisi od koeficijenta k, tj. koeficijenta pravca prave. Ako je k>0 funkcija je rastuća, tj. sa x-osom zaklapa oštar ugao, a ako je k<0 funkcija je opadajuća, tj. sa x-osom zaklapa tup ugao.
Funkcija y=kx+n
Da bismo proučili ovu funkciju, odaberimo da je prvo k>0 i x1<x2; x1<x2 ⇒ kx1+n < kx2+n ⇒ y1<y2.
U ovom slučaju funkcija je rastuća u skupu R.
Funkcija y=kx+n ima vrijednost 0 ako je kx+n = 0, odnosno x = -n/k. Ovu vrijednost promjenljive x nazivamo nula funkcije.
Da bismo ispitali znak funkcije, napišimo je u obliku y = k(x+n/k), dakle:
1. x+n/k > 0 ⇒ x > -n/k (razmatramo nulu funkcije)
2. x+n/k < 0 ⇒ x < -n/k (razmatramo nulu funkcije)
U oba slučaja k>0, funkcija ima znak jednak znaku faktora (x+n/k) tako da je u prvom slučaju funkcija pozitivna za navedene vrijednosti promjenljive x (koje su veće od nule funkcije), a negativna za one vrijednosti promjenljive x koje su manje od nule funkcije.
Sada uzmimo da je k<0 i x1<x2; x1<x2 ⇒ kx1 > kx2 ⇒ kx1+n > kx2+n ⇒ y1>y2.
U ovom slučaju funkcija opada jer manjim vrijednostima promjenljive x odgovaraju veće vrijednosti funkcije y.
Ispitajmo znak funkcije na isti način, napišimo je u obliku y = k(x+n/k), dakle:
1. x+n/k > 0 ⇒ x > -n/k (razmatramo nulu funkcije)
2. x+n/k < 0 ⇒ x < -n/k (razmatramo nulu funkcije)
U oba slučaja k<0, funkcija ima znak suprotan znaku faktora (x+n/k) tako da je u prvom slučaju funkcija negativna za navedene vrijednosti promjenljive x (koje su veće od nule funkcije), a pozitivna za one vrijednosti promjenljive x koje su manje od nule funkcije.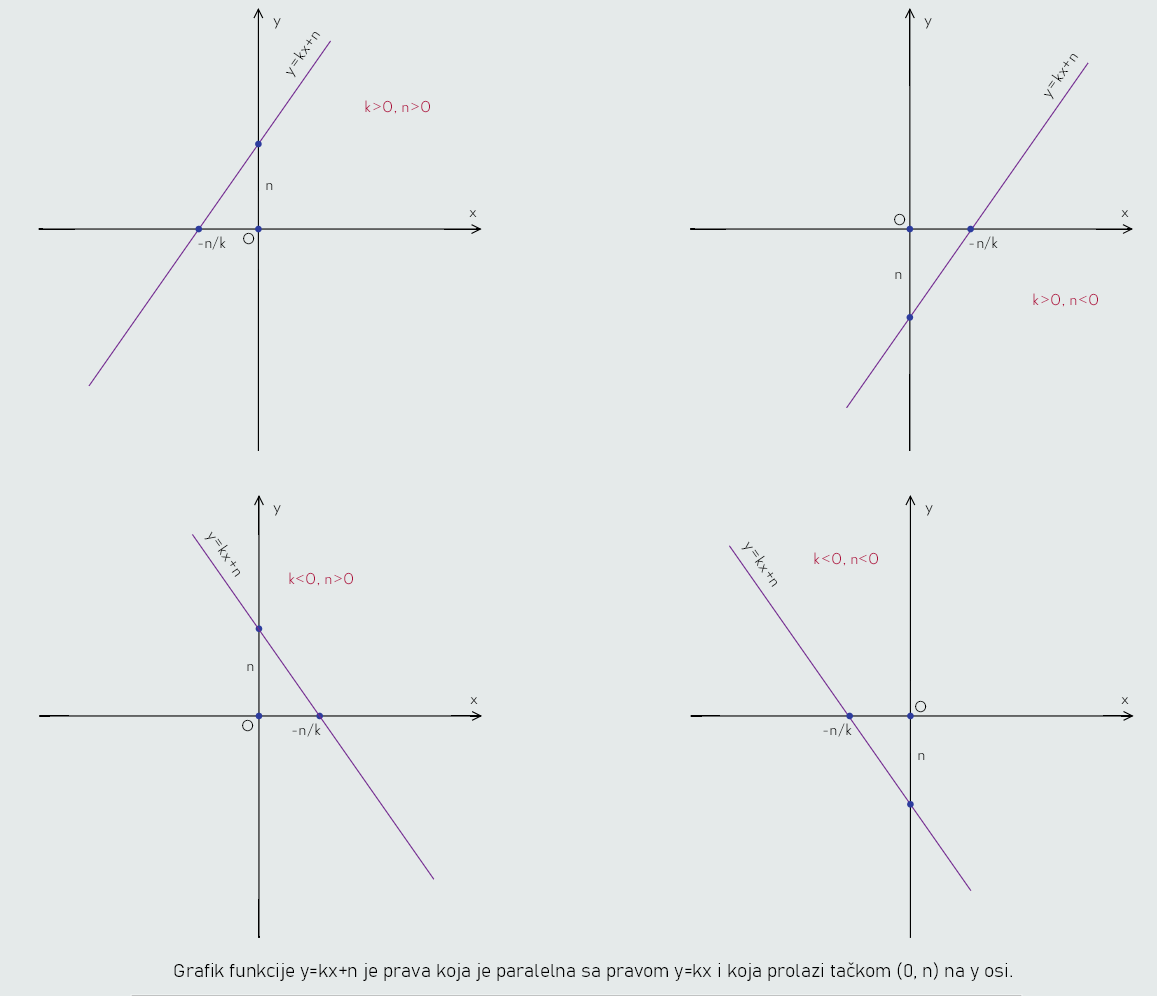
Funkcija obrnute proporcionalnosti y=k/x, (k≠0)
Kod ove funkcije vrijedi da je y1:y2 = k/x1 : k/x2 = x2:x1, odnosno y1 i y2 su obrnuto proporcionalne odgovarajućim vrijednostima x1 i x2.
Funkcija y=k/x definisana je za sve realne vrijednosti promjenljive x osim za x=0.
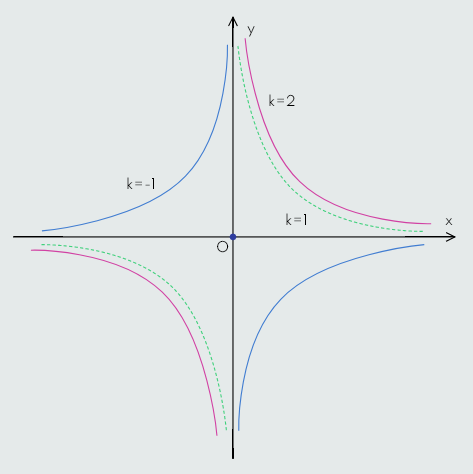
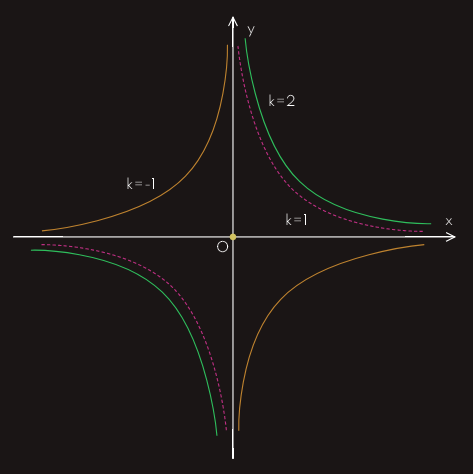
Kada je k>0 funkcija ima znak promjenljive x, a u slučaju k<0 funkcija ima znak suprotan znaku promjenljive x.
Na sljedećoj slici su prikazane funkcije za k=1, k=2 i k=-1.