Teorema: Površina trougla jednaka je polovini proizvoda dužina njegove stranice i visine koja odgovara toj stranici.
PABC = a·ha/2 = b·hb/2 = c·hc/2
Posljedica: Površina pravouglog trougla jednaka je polovini proizvoda dužina njegovih kateta.
Teorema: Površina trapeza jednaka je proizvodu poluzbira dužina njegovih osnovica i dužine visine.
PABCD = [(a+c)/2]·h
Posljedica: Površina trapeza jednaka je proizvodu dužina srednje linije i visine trapeza.
Koordinatni sistem
Dekartov proizvod dva skupa
Skup od dva elementa naziva se par.
Ako su elementi ovog skupa a i b, onda se takav skup označava sa {a,b} ili {b,a} i vrijedi da je {a,b} = {b,a}. Međutim, u određenim situacijama nam je redoslijed elemenata važan, bitno je koji elemenat u paru je na prvom, a koji na drugom mjestu. U ovoj situaciji za par kažemo da je uređen; pri čemu ako je elemenat a na prvom, a elemenat b na drugom mjestu, skup označavamo (a,b).
Elemenat a je prva komponenta ili prva koordinata, a elemenat b je druga komponenta ili druga koordinata para.
Vrijedi jednakost:
(a,b) = (c,d) ⇔ a=c ∧ b=d.
Neka su sada data dva skupa A={a,b,c} i B={1,5,7}.
Formirajmo sve uređene parove koji imaju prvu komponentu iz skupa A, a drugu iz skupa B, i skup tih parova označimo sa AxB:
AxB={(a,1), (a,5), (a,7), (b,1), (b,5), (b,7), (c,1), (c,5), (c,7)}.
Skup AxB naziva se Dekartov proizvod skupa A i skupa B.
U općem slučaju AxB = {(x,y)| x∈A ∧ y∈B}. 
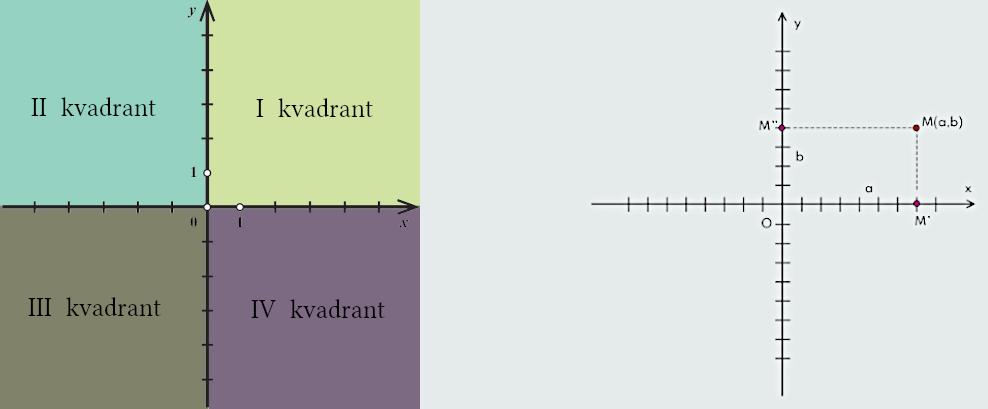
Dekartov koordinatni sistem u ravni određuju dva međusobno okomita brojevna pravca koja nazivamo koordinatne ose.
Horizontalnu osu nazivamo osa x ili apscisa. Vertikalnu osu nazivamo osa y ili ordinata.
Sjecište koordinatnih osa nazivamo ishodište koordinatnog sistema.
Svaki elemenat (x,y) Dekartovog proizvoda RxR određuje jednu tačku T ravni i obratno; kažemo da su (x,y) koordinate tačke T i zapisujemo T(x,y). Broj x nazivamo apscisa tačke T, a broj y ordinata tačke T.
Kvadranti i tačke na osama
Koordinatne ose dijele ravan na četiri dijela koja nazivamo kvadranti.

Linearna funkcija
Ranije smo se već upoznali sa pojmom funkcije, vidjeli smo da zavisnost broja y od odabira broja x možemo napisati u obliku y=f(x), gdje f predstavlja pravilo pridruživanja (slovo f je zato što riječ "pravilo" u latinskom jeziku se iskazuje sa "functio", tj. funkcija). Pod pojmom funkcija podrazumijevamo pravilo pridruživanja u kojem vrijednosti jedne veličine pridružujemo tačno jednu vrijednost druge veličine. Funkcija je najčešće zadana formulom, tablicom ili grafičkim prikazom. S obzirom na to da je vrijednost druge veličine (veličine y) potpuno određena vrijednošću prve veličine (veličine x) i funkcijom f, pišemo y=f(x).
Linearna funkcija je pridruživanje kojem nekom racionalnom broju x pridružujemo racionalni broj f(x), a pravilo pridruživanja zadano je formulom f(x)=ax+b, pri čemu je a≠0.
Brojeve a i b nazivamo koeficijentima ili parametrima linearne funkcije. Broj x je nezavisna veličina i zovemo ga argument linearne funkcije. Broj f(x) je vrijednost funkcije f za zadani argument x.
Funkcija direktne proporcionalnosti y=kx
Kada su dvije veličine direktno proporcionalne, tada je njihov odnos stalan broj; (y⁄x = k), odnosno y = kx, k je konstanta. Dakle, svakoj vrijednosti varijable x odgovara tačno jedna vrijednost varijable y, tj. imamo jednu funkciju (preslikavanje) definisanu na prvom skupu čije su vrijednosti u drugom skupu.
Ovom relacijom, y=kx predstavljena je funkcija koju nazivamo funkcija direktne proporcionalnosti.
Kada imamo x1 i x2, odnosno y1 i y2, za koje je y1 = kx1 i y2 = kx2, slijedi da je:
y1/x1 = k i y2/x2 = k, odnosno y1/x1 = y2/x2, što možemo napisati u obliku: y1:x1 = y2:x2 i ova se jednakost naziva proporcija, pri čemu su y1, x1, y2, x2 članovi proporcije, i to y1 i x2 - vanjski članovi, a x1 i y2 - unutrašnji članovi. Takođe možemo ovu proporciju napisati i u drugačijem obliku: y1:y2 = x1:x2, koji dobivamo polazeći od početnih relacija y1 = kx1 i y2 = kx2. Dalje, od ovih početnih relacija, kombiniranjem možemo dobiti jednakost: (kx1)·y2 = y1·(kx2) ⇒ x1·y2 = y1·x2, gdje vidimo da je proizvod unutrašnjih članova proporcije jednak proizvodu njenih vanjskih članova.
Dvije proporcije koje imaju osobinu da im je proizvod unutrašnjih i spoljašnjih članova isti broj nazivaju se ekvivalentne proporcije.
Ako se u proporciji pojavljuju dva jednaka unutrašnja ili vanjska člana, tada se taj član naziva geometrijska proporcionala ili geometrijska sredina preostala dva člana proporcije, npr:
9:3 = 3:1, broj 3 je geometrijska sredina brojeva 9 i 1.
U opštem slučaju, a je geometrijska sredina od b i c ako vrijedi b:a = a:c, a2 = b·c ⇒ a = √(b·c).
Svaka se funkcija može grafički predstaviti u pravouglom koordinatnom sistemu, pri čemu vrijednost varijable x predstavljamo na apscisi, a odgovarajuće vrijednosti varijable y na ordinati.