Vektori u ravni
Pojam skalara i vektora
Neke veličine u geometriji, fizici, hemiji itd. određene su sa jednom brojnom vrijednošću, jednim realnim brojem; takve su npr. veličine: masa, temeperatura, dužina, površina, zapremina i sl. - ove veličine nazivamo skalari.
S druge strane, veličine koje nisu određene samo brojem, nego za njihovu potpunu određenost moramo poznavati i pravac i smjer, kao što je npr. brzina (potrebno je poznavati pravac u kojem se tijelo kreće i smjer kretanja), nazivamo vektorske veličine ili vektori.
Vektorske veličine predstavljamo grafički sa duži čiji su krajevi uređeni - znamo koji kraj duži je prvi, a koji drugi; takva je duž orijentisana duž ili vektor. 

Jednaki i suprotni vektori
Definicija: Ako dva vektora pripadaju paralelnim pravima, za njih kažemo da imaju isti pravac ili da su kolinearni. 


Sabiranje i oduzimanje vektora
Zbir vektora
Vektori se nadovezuju jedan na drugi tako da je kraj jednog vektora početak drugog, kraj drugog je početak trećeg vektora itd. Kada spojimo početak prvog vektora i kraj zadnjeg od nadovezanih vektora dobijamo vektor koji predstavlja zbir posmatranih vektora. 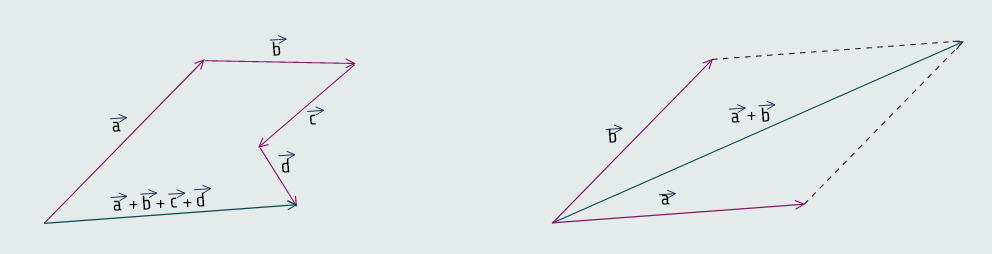
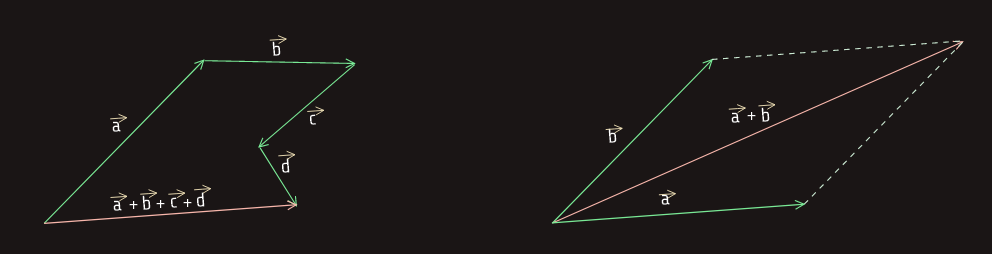
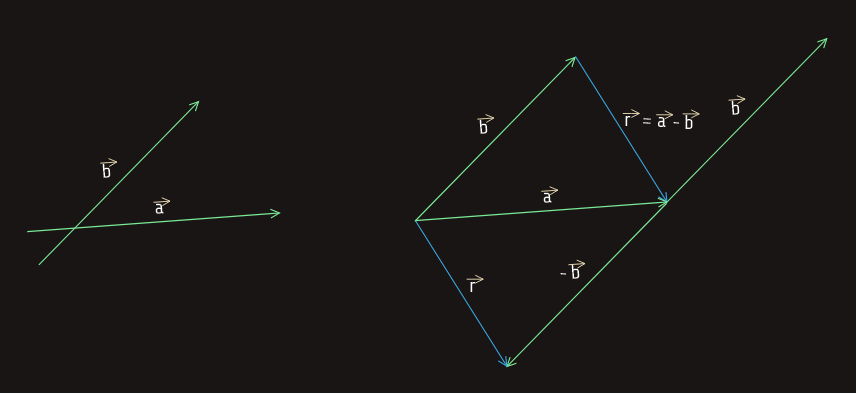
Razlika vektora
Neka su dati vektori a i b . Vektor r za koji vrijedi da je a = b + r nazivamo razlika vektora a i b , i pišemo: r = a - b . 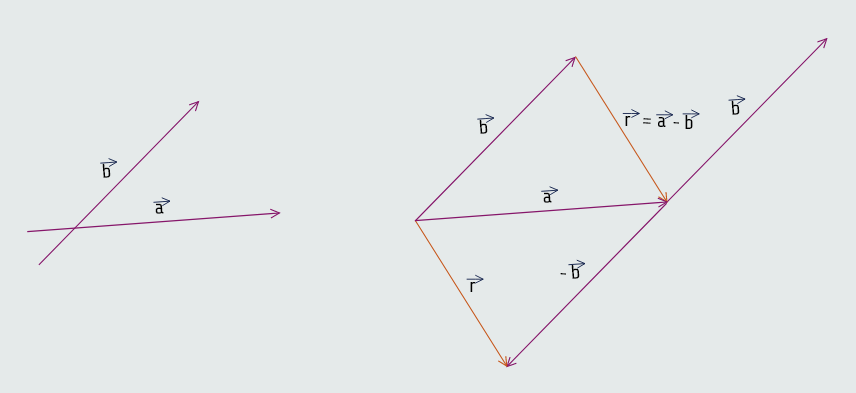
Srednja duž trougla
Definicija: Duž čiji su krajevi središta dviju stranica trougla nazivamo srednja duž trougla. 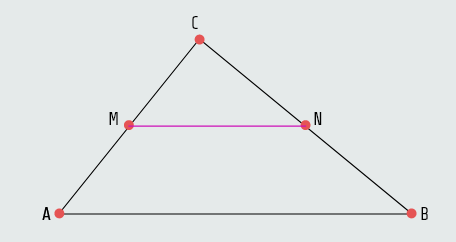
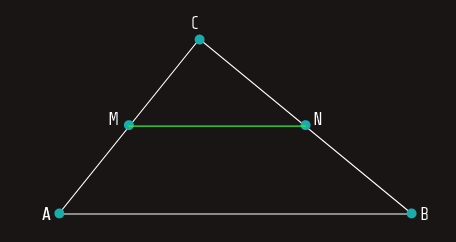
Dokaz: Dokažite teoremu koristeći se vektorima...
Izometrijska preslikavanja u ravni
Ako svakom elementu jednog skupa na neki način pridružimo element drugog skupa, tada kažemo da smo prvi skup preslikali u drugi skup, a postupak nazivamo funkcija sa prvog skupa u drugi. Kada su posmatrani skupovi - skupovi tačaka, funkciju nazivamo transformacija.
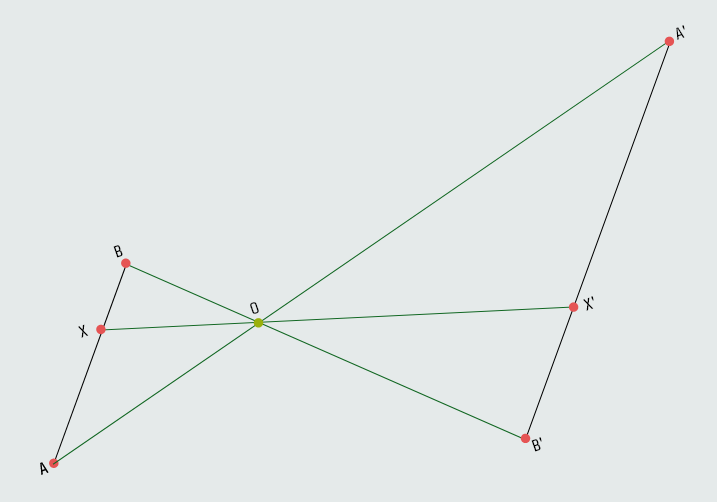
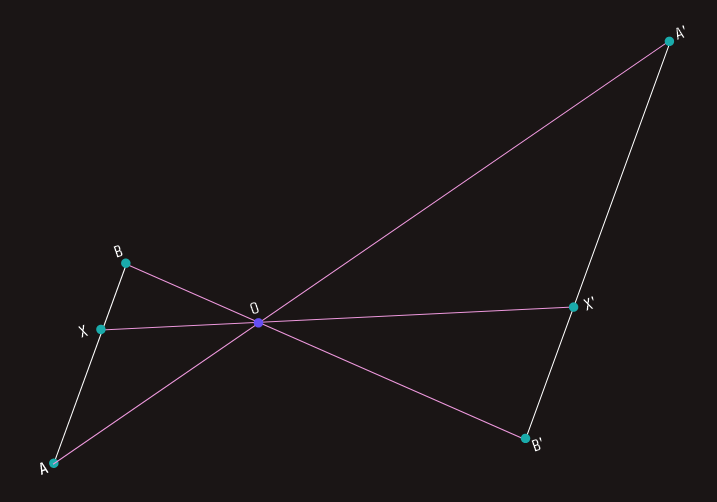
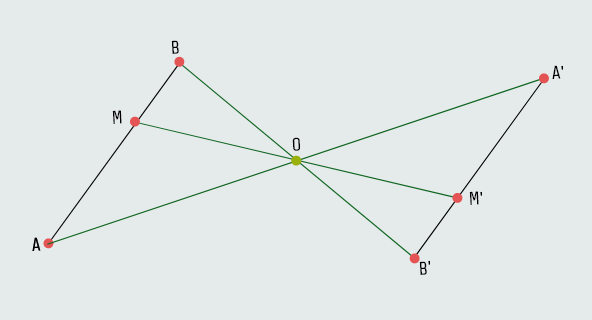
Primjer-1: Neka je data duž AB i tačka O van te duži; neka je tačka M bilo koja tačka navedene duži. Pridružimo tački M tačku M' tako da tačka O bude središte duži MM'. Ako svakoj tački X duži AB na isti način pridružimo tačku X', dobićemo duž A'B' koja je po svemu jednaka duži AB - dužina duži je ostala ista, samo je duž AB promijenila položaj; dakle, duž AB se transformisala u duž A'B'.
Primjer-2: Ako uzmemo ponovo duž AB i tačku O van te duži i neka je tačka X bilo koja tačka navedene duži. Pridružimo tački X tačku X' tako da tačka O bude između tačaka X i X' i to tako da je udaljenost tačke O od tačke X' dva puta veća od udaljenosti tačke O od tačke X. Duž AB će se na ovaj način transformisati u duž A'B', pri čemu je jasno da ove dvije duži sada nemaju jednake dužine.
Prilikom transformacije jednog skupa tačaka u drugi, odnosno jedne figure u drugu, osobine prve i druge figure mogu biti iste, mogu se razlikovati ili može biti da su neke osobine iste, a druge različite.