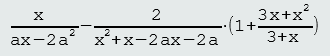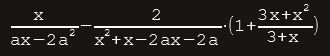Posmatraćemo ovdje polinome sa jednom promjenljivom, tako da ako je varijabla x, a stepen polinoma n, tada polinom Pn(x) definišemo na sljedeći način:
Pn(x)=anxn+an-1xn-1+an-2xn-2+ ... +a2x2+a1x+a0
Tako je za polinom:
P7(x)=4x7+x6+x4-x3+3x2+9 stepen polinoma 7, dok je za:
P0(x)=223 stepen polinoma 0.
Polinomi Pn(x)=anxn+an-1xn-1+an-2xn-2+ ... +a2x2+a1x+a0 i Qm(x)=bmxm+bm-1xm-1+bm-2xm-2+ ... +b2x2+b1x+b0 su jednaki ako i samo ako vrijedi:
1. n=m
2. a0=b0, a1=b1, a2=b2, ..., an=bn
Sabiranje, oduzimanje i množenje polinoma
Sabiranje polinoma izvodimo tako što saberemo sve slične članove i od njih formiramo novi polinom koji zovemo zbir datih polinoma. Na ovakav način dobivamo i razliku polinoma ako umjesto operacije sabiranja radimo sa operacijom oduzimanja jednog polinoma od drugog.
Najbolje ćemo to uočiti na sljedećem primjeru.
Zadatak:
Ako su dati polinomi P3(x)=2x3-3x2+4x-5 i Q4(x)=x4-x3+2x2+x-1, odrediti zbir i razliku datih polinoma.
Rješenje:
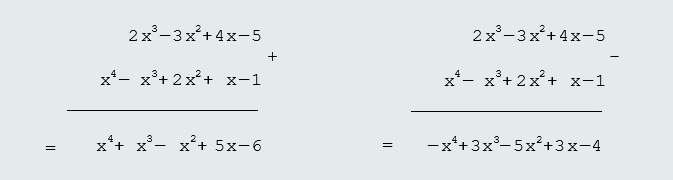
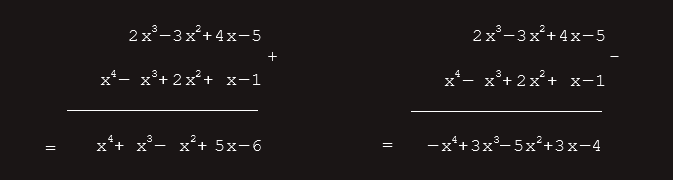
Množenje polinoma zasniva se na zakonu distributivnosti množenja prema sabiranju i oduzimanju brojeva:
(a+b)·c=ac+bc
(a-b)·c=ac-bc
a·(b+c)=ab+ac
a·(b-c)=ab-ac a,b,c∈R
Umjesto brojeva a,b,c uzimamo bilo koje polinome.
Primjer:
(2x4-x3-x-1)·(x2-5) = 2x4(x2-5)-x3(x2-5)-x(x2-5)-(x2-5) = 2x4x2-10x4-x3x2+5x3-xx2+5x-x2+5 = 2x6-10x4-x5+5x3-x3+5x-x2+5 = 2x6-x5-10x4+4x3-x2+5x+5
Rastavljanje polinoma na faktore
Rastaviti broj na faktore znači napisati ga u obliku proizvoda više brojeva. Obično rastavljamo broj na proste faktore, odnosno složen broj pišemo u obliku proizvoda prostih brojeva.
Na primjer 105=3·5·7.
Polinome rastavljamo na faktore na identičan način, tj. polinom smo rastavili na faktore ako smo ga napisali u obliku proizvoda drugih polinoma. Tako je na primjer:
4x3+12x=4x(x2+3)
2ab+2ac-2ad+2ax=2a(b+c-d+x)
ax-by+bx-ay=ax-ay+bx-by=a(x-y)+b(x-y)=(a+b)(x-y)
a2+a-6=a2+3a-2a-6=a(a+3)-2(a+3)=(a+3)(a-2) itd.
Kvadrat i kub binoma
Neke proizvode u zadacima tako često susrećemo da ih je korisno istaći i zapamtiti kao odgovarajuće formule.
Za realni broj a vrijedi da je an=a·a···a (n puta).
Ako su (a,b)∈R, vrijedi da je am·an=am+n, (ab)n=anbn pri čemu su m i n prirodni brojevi.
Ako umjesto proizvoda a i b imamo (a+b) ili (a+b+c), tada govorimo o binomu, odnosno trinomu.
Za sve realne brojeve a i b vrijedi da je (a+b)2=a2+2ab+b2 , što predstavlja formulu za kvadrat zbira (binoma). Odnosno, iskazano riječima; kvadrat binoma je zbir kvadrata prvog člana, dvostrukog proizvoda prvog i drugog člana i kvadrata drugog člana.
Dakle, imamo:
(a+b)2=(a+b)(a+b)=a2+ab+ba+b2=a2+2ab+b2
Na sličan način, za kvadrat razlike imamo:
(a-b)2=a2-2ab+b2
Iz prethodna dva izraza smo zapravo kvadrat binoma napisali kao trinom; zaključujemo da izraz (trinom) možemo napisati kao kvadrat binoma. Tako je npr. x2+6x+9=(x+3)2.
Dalje, za realne brojeve a i b vrijedi da je (a+b)3=a3+3a2b+3ab2+b3 i ova formula predstavlja formulu za kub binoma.
Možemo je izvesti na način:
(a+b)3=(a+b)(a+b)(a+b)=(a2+2ab+b2)(a+b)=a3+a2b+2a2b+2ab2+ab2+b3=a3+3a2b+3ab2+b3
Ako imamo razliku, tada je (a-b)3=a3-3a2b+3ab2-b3 .
Razlika kvadrata i razlika kubova
Za razliku kvadrata imamo a2-b2=(a-b)(a+b) .
Kod razlike kubova vrijedi a3-b3=(a-b)(a2+ab+b2) ,
dok je kod zbira kubova a3+b3=(a+b)(a2-ab+b2)
Kažimo još da je generalno:
(a+b+c+...+z)x=ax+bx+cx+...+zx
(a+b+c+...+z)(x+y)=(ax+bx+cx+...+zx)+(ay+by+cy+...+zy)
Algebarske izraze je moguće transformisati primjenom osobina operacija sa cijelim algebarskim izrazima. Transformaciju radimo zbog dovođenja izraza na što jednostavniji oblik, dokazivanja jednakosti dvaju izraza, dokazivanja određene relacije između izraza pod datim uslovima i sl.
Zadatak: Pomnožimo (a+3)(b+2) i nacrtajmo rezultat.
Rješenje:
(a+3)(b+2)=a(b+2)+3(b+2)=ab+2a+3b+6 
Racionalni algebarski izrazi
Ako algebarski izraz sadrži operacije sabiranje, oduzimanje, množenje, stepenovanje sa cijelim eksponentom i dijeljenje naziva se racionalni algebarski izraz ili algebarski razlomak. Drugim riječima, racionalni algebarski izraz predstavlja količnik dvaju polinoma, Pn(x)⁄Qm(x), Qm(x)≠0. Svaki cijeli algebarski izraz je u suštini samo specijalan slučaj racionalnog algebarskog izraza. Na primjer:
(a2-2a+1)⁄(a-3) je definisan za (a-3)≠0, a≠3, odnosno nije definisan za a=3.
(3a+5)⁄(x2+1) je uvijek definisan jer x2+1 nikada nije jednako 0.
Sabiranje, oduzimanje, množenje i dijeljenje racionalnih algebarskih izraza
Sve osobine racionalnih brojeva a⁄b koje smo vidjeli ranije, vrijede i za algebarske racionalne izraze Pn(x)⁄Qm(x), Qm(x)≠0.
Skratiti ili proširiti racionalni izraz znači podijeliti ili pomnožiti mu i brojnik i nazivnik istim izrazom, respektivno.
Na primjer: (6a3b3)⁄(8a4b) = 3b2/4a, pri čemu smo razlomak skratili sa 2a3b, odnosno razlomak (2a-1)⁄(a+3) proširivanjem sa (a-5) pišemo u obliku ((2a-1)(a-5))⁄((a+3)(a-5)).
Sabiranje ili oduzimanje razlomaka radimo na način da im nađemo zajednički nazivnik (ako nazivnici nisu jednaki) i onda sabiramo ili oduzimamo brojnike.
Na primjer: (a/2x) - (b/3y) + (2a/3x) - (b/2y) = (3ay-2bx+4ay-3bx)/6xy = (7ay-5bx)/6xy
Proizvod dva ili više razlomaka je razlomak čiji je brojnik jednak proizvodu brojnika, a nazivnik proizvodu nazivnika datih razlomaka:
[A(x)⁄B(x)] · [C(x)⁄D(x)] = [A(x)·C(x)]⁄[B(x)·D(x)], B(x)≠0, D(x)≠0.
Količnik dva algebarska razlomka definišemo na sljedeći način:
[A(x)⁄B(x)] : [C(x)⁄D(x)] = [A(x)⁄B(x)] · [D(x)⁄C(x)] = [A(x)·D(x)]⁄[B(x)·C(x)], B(x)≠0, C(x)≠0, D(x)≠0.
Napomena:
Kada radimo transformaciju algebarskih racionalnih izraza, potrebno je voditi računa o redoslijedu operacija kao i o postupnosti u dovođenju izraza na najjednostavniji oblik.
Zadatak za vježbu:
Pokušajte od sljedećeg izraza dobiti rezultat 1/a: