Primjer-3: Posmatrajmo sada kružnicu sa centrom u tački O i duž AB koja ne pripada pravoj koja prolazi kroz centar kružnice. Tačke A i O određuju pravu koja siječe kružnicu u nekoj tački (A'), dok tačke B i O određuju pravu koja ima presječnu tačku (B') sa kružnicom. Svakoj unutrašnjoj tački X duži AB pridružimo tačku X' koja se nalazi na presjeku prave OX i date kružnice. Ovakvim načinom se duž AB transformisala u dio kružnice - luk A'B' pri čemu ova transformacija ne samo da ne zadržava udaljenost između tačaka, nego mijenja i sam oblik figure, odnosno duž preslikava u luk.
Definicija: Transformacija ravni ili preslikavanje ravni u samu sebe koja čuva rastojanje između tačaka nazivamo izometrija ili izometrijsko preslikavanje.
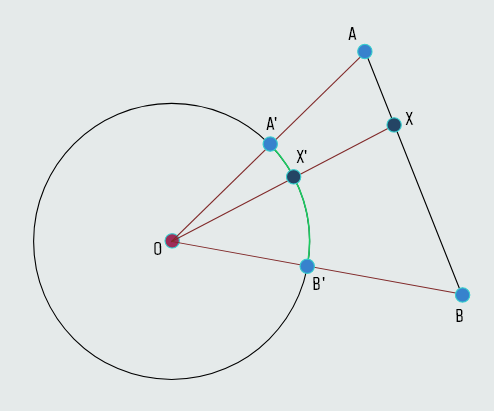
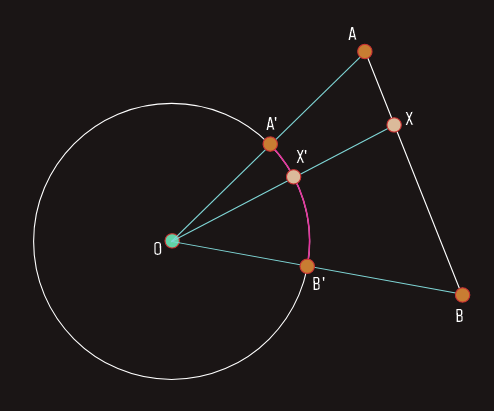
Translacija u ravni
Neka je u ravni poznat vektor v . Sada uzmimo nekoliko tačaka A, B, C, D, ... X... te ravni i odredimo tačke A', B', C', D', ... X'... tako da bude AA' = v , BB' = v , CC' = v , DD' = v , ... XX' = v ... 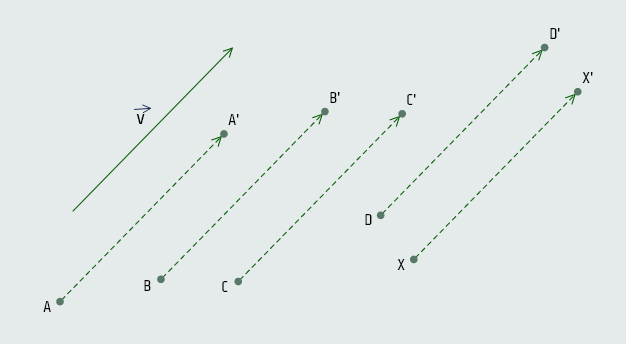
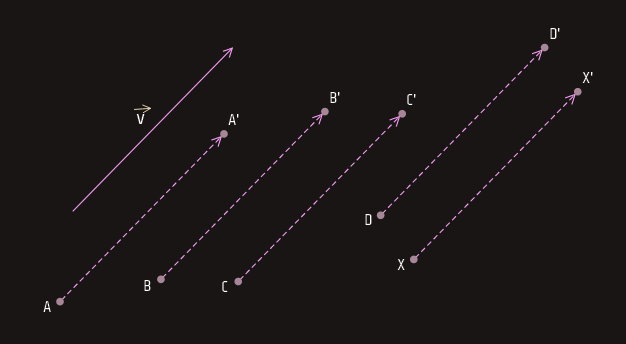
Definicija: Transformacija koja svakoj tački M ravni pridružuje tačku M' te ravni tako da je vektor MM' jednak datom vektoru v naziva se translacija za vektor v .
Vektor v nazivamo vektor translacije.
Teorema: Translacija je izometrija.
Dokaz: Neka je data translacija za vektor v , i neka se tačka A translatira u A' i B u B'. Tada vrijedi da je:
AA' = v i BB' = v , pa je AA' = BB' .
Iz ove relacije slijedi da je AB = A'B' .
Translacija, dakle, ne mijenja udaljenost između tačaka; sve osobine izometrije vrijede i za translaciju - translacija ima i dodatno osobinu da pravu preslikava u paralelnu pravu.
Rotacija u ravni
Uglove koje smo do sada obradili nazivamo neorijentisanim uglovima, međutim ako uzmemo da kraci ugla nisu ravnopravni i da je jedan od njih prvi, a preostali krak drugi, tada kažemo da je ugao orijentisan, i to pozitivno ili negativno, kako prikazuje donja slika: 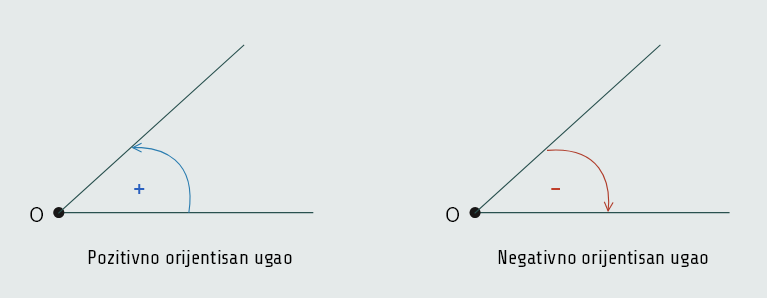
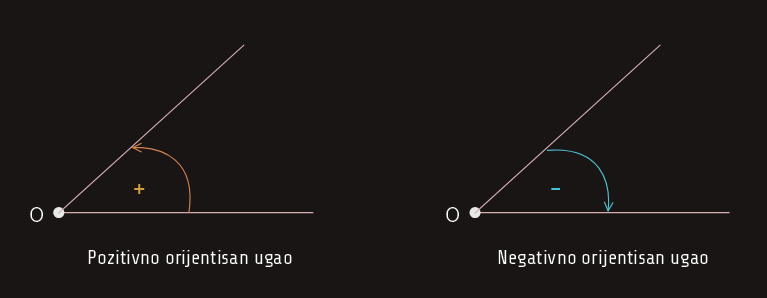
Neka je dat jedan orijentisani ugao α i jedna tačka O ravni. Ako uzmemo bilo koju tačku M ravni, onda ovoj tački možemo pridružiti tačku M' tako da vrijedi:
OM' = OM i ∠MOM' = α.
Ovdje govorimo o rotaciji tačke M oko tačke O za dati orijentisani ugao α.
Ako bi na isti način izvršili rotaciju svake tačke ravni, tada bismo kazali da je izvršena rotacija ravni oko tačke O za ugao α.
Definicija: Transformacija ravni koja svakoj tački M te ravni pridružuje tačku M' iste ravni tako da je MO = M'O i ∠MOM' = α, gdje je O data tačka, a α dati orijentisani ugao, naziva se rotacija oko tačke O za ugao α.
Teorema: Rotacija je izometrija.
Dokaz: Neka rotacija oko tačke O za dati ugao α tački A pridružuje tačku A' i tački B tačku B'. 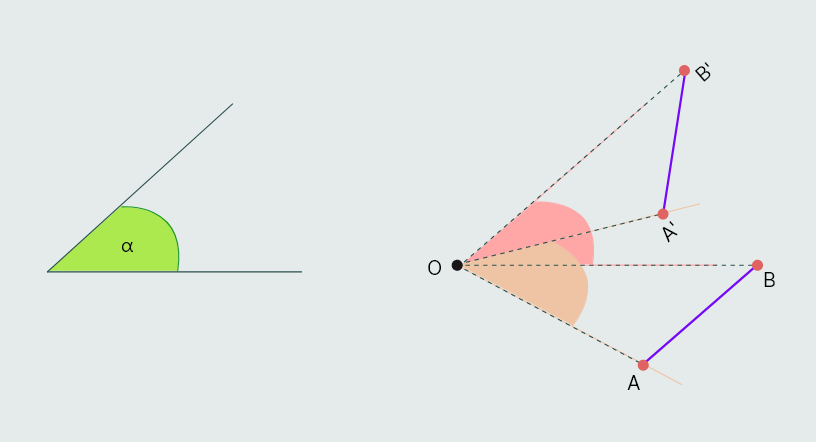
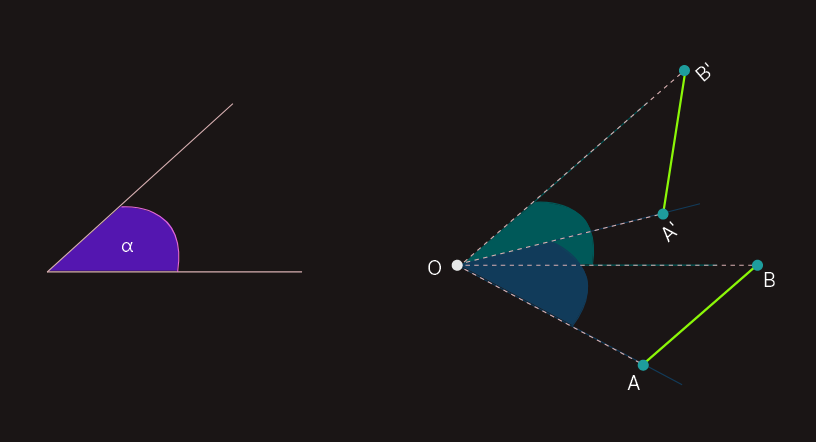
Dakle, prema definiciji rotacije, imamo da je OA = OA' i OB = OB', ∠AOA' = ∠BOB' = α.
Dalje, sa slike vidimo da je:
∠AOB = α - ∠BOA' = ∠AOA'- ∠BOA'
∠A'OB' = α - ∠BOA' = ∠BOB'- ∠BOA'
Dakle, ugao ∠AOB = ∠A'OB'.
Na osnovu stava SUS (stranica-ugao-stranica) trouglovi AOB i A'OB' su podudarni, iz čega slijedi da im je i treća stranica jednaka, tj. AB = A'B', čime je dokazano da rotacija čuva rastojanje između tačaka, odnosno da je rotacija izometrija.
Primjena translacije i rotacije
Unakrsni uglovi
Definicija: Dva ugla kod kojih su kraci jednog dopune krakova drugog do pravih, nazivaju se unakrsni uglovi. 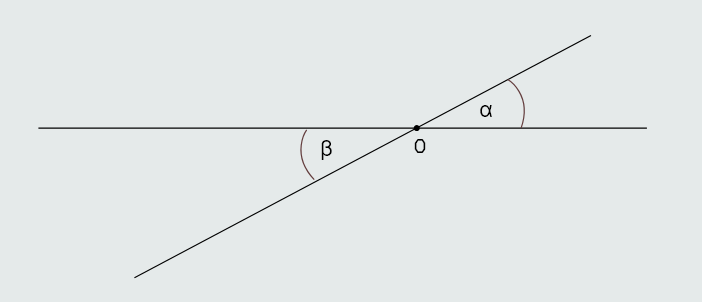
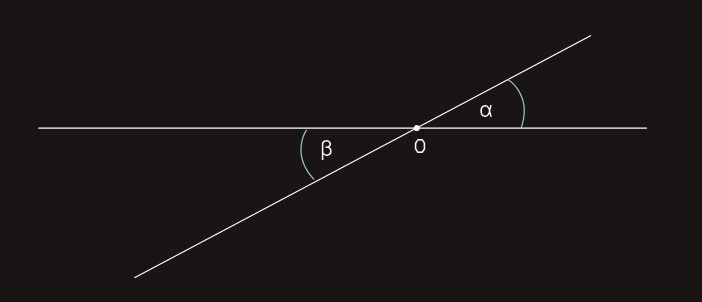
Dokaz: Rotacija oko vrha O za 180° preslikava ugao α u ugao β, što dokazuje jednakost uglova.