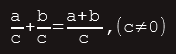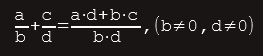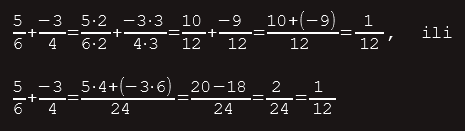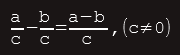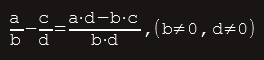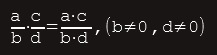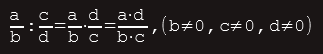Cijeli brojevi (Z)
Cijeli brojevi uvedeni su iz teorijskih, naučnih i praktičnih razloga. Računanjem sa prirodnim brojevima za operaciju oduzimanja, često možemo doći do zaključka da se nešto ne može izračunati i da nema rješenja. Ako recimo pogledamo jednu naizgled jednostavnu jednačinu:
x+5=3
U skupu N ova jednačina nema rješenja. Ne postoji nijedan prirodan broj čiji je zbir s brojem 5 jednak broju 3. Dakle, nametnula se potreba da se skup prirodnih brojeva proširi sa drugim elementima, tako da novi skup:
..., -(n+1),-n,..., -4, -3, -2, -1, 0, 1, 2, 3, 4,..., n, n+1,...
gdje je n prirodan broj, zovemo skup cijelih brojeva koji označavamo sa Z.
Vidimo da je skupu N dodana 0 i da za svaki prirodan broj postoji još jedan broj koji njemu odgovara, te je tako nastao skup Z.
Z = {..., -(n+1),-n,..., -4, -3, -2, -1, 0, 1, 2, 3, 4,..., n, n+1,...}
Brojevi desno od nule (prirodni brojevi) su u skupu Z pozitivni cijeli brojevi, dok su brojevi lijevo od nule negativni cijeli brojevi.
Sabiranje cijelih brojeva definira se na sljedeći način:
x+(-y)=x-y, ako je x>y (x, y ∈ N)
x+(-y)=-(y-x), ako je y>x (x, y ∈ N)
Tako je na primjer:
5+(-3)=5-3=2
3+(-7)=-(7-3)=-4
4+11=15
(-6)+(-9)=-(6+9)=-15
U skupu cijelih brojeva vrijede relacije:
1. x+0=x
2. x+(-x)=0
3. x+y=y+x (zakon komutacije za sabiranje)
4. x+(y+z)=(x+y)+z (zakon asocijacije za sabiranje)
Sljedeće se osobine cijelih brojeva mogu dokazati:
1. -(-x)=x (∀x∈Z)
2. Jednačina x+a=b ima tačno jedno rješenje x=b+(-a)=b-a
3. -(x+y)=-x-y (∀x,y∈Z)
4. -(x-y)=-x+y (∀x,y∈Z)
5. (-x)+(-y)=-(x+y) (∀x,y∈Z)
Cijeli brojevi x i -x zovu se suprotni brojevi.
U skupu cijelih brojeva oduzimanje se može izvoditi bez ograničenja. Tako npr. prethodna jednačina x+5=3, koja u skupu N nema rješenja, ovdje, u skupu Z ima rješenje:
x=3-5
x=3+(-5)=-(5-3)=-2
Množenje pozitivnih cijelih brojeva izvodi se kao i množenje prirodnih brojeva. Za množenje cijelih brojeva vrijede sljedeće tvrdnje:
1. 1·x=x (∀x∈Z)
2. x·y=y·x (∀x,y∈Z) (zakon komutacije)
3. (x·y)·z=x·(y·z) (∀x,y∈Z) (zakon asocijacije)
4. x·(y+z)=x·y+x·z (∀x,y∈Z) (zakon distribucije množenja u odnosu na sabiranje)
Takođe, za cijele brojeve vrijede i sljedeće osobine koje se mogu dokazati:
1. x·0=0 (∀x∈Z)
2. x·(-y)=-x·y (∀x,y∈N)
3. (-x)·y=-x·y (∀x,y∈N)
4. (-x)·(-y)=x·y (∀x,y∈N)
Osobinu 1., na primjer, možemo dokazati ako krenemo od očite jednakosti x·a-x·a=0.
Primjenimo li sada zakon distribucije množenja u odnosu na sabiranje i osobinu zbira dva suprotna broja, imamo:
x·(a-a)=0
x·0=0
Za svaki cijeli broj uvodi se pojam apsolutne vrijednosti. Apsolutna vrijednost cijelog broja definiše se na sljedeći način:
∣0∣=0
∣x∣=x (x∈N)
∣-x∣=x (x∈N)
Tako je na primjer: ∣31∣=31, ∣-7∣=7, ∣44∣=44...
Racionalni brojevi (Q)
Operacija dijeljenje je uslovna u skupu cijelih brojeva. Bilo je potrebno da se skup brojeva dalje širi, odnosno ukazala se potreba za brojevima koji nisu "cijeli", te su tako uvedeni razlomci. Razlomke pišemo u obliku a:b ili a⁄b, gdje su a i b cijeli brojevi i b≠0. Broj a se zove brojnik, a broj b nazivnik razlomka.
Napomena: Notacija a⁄b zapravo predstavlja oblik 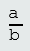
Primjer razlomaka: 2⁄4, -5⁄15, 0⁄8, 60⁄-5, ...
Skup svih razlomaka oblika a⁄b gdje su a i b cijeli brojevi i b≠0 nazivamo skup racionalnih brojeva koji označavamo sa Q:
Q = {a⁄b; a,b∈Z, b≠0}
Primjetimo da svaki cijeli broj možemo napisati u obliku razlomka, što znači da su i cijeli brojevi racionalni.
Za dva razlomka a⁄b i c⁄d kažemo da su jednaki ako vrijedi a⋅d=b⋅c.
a⁄b = c⁄d ⇔ a⋅d=b⋅c
Razlomke možemo proširivati ili skraćivati, npr. brojem c (c≠0).
Ako razlomak a⁄b napišemo u obliku ac⁄bc, kažemo da smo razlomak a⁄b proširili sa c, a razlomak smo skratili sa c ako ac⁄bc napišemo u obliku a⁄b. Drugim riječima, kod proširivanja razlomka, množimo i brojnik i nazivnik istim brojem, dok kod skraćivanja i brojnik i nazivnik dijelimo sa istim brojem, različitim od nule.
Sabiranje razlomaka
a. Razlomci jednakih nazivnika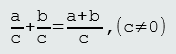
Dva razlomka jednakih nazivnika sabiramo tako što odredimo treći razlomak čiji je brojnik jednak zbiru dva brojnika pomenutih razlomaka, a nazivnik jednak nazivniku razlomaka koje sabiramo.
b. Razlomci nejednakih nazivnika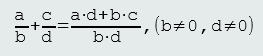
U ovom slučaju, radimo proširivanje razlomaka pogodno odabranim brojevima, tako da oni nakon proširivanja imaju jednake nazivnike i onda sabiramo razlomke na prethodno opisan način.
Na primjer: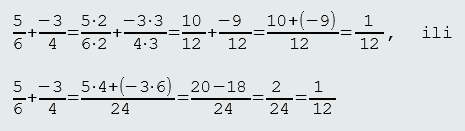
Oduzimanje razlomaka
Oduzimanje razlomaka izvodimo na sljedeći način:
a. Razlomci jednakih nazivnika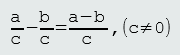
b. Razlomci nejednakih nazivnika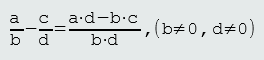
Množenje racionalnih brojeva (razlomaka) definišemo: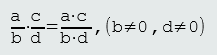
Svakom racionalnom broju r odgovara broj r' za koji vrijedi r·r'=1 i taj broj nazivamo recipročan broj broja r.
Dakle, r'=1⁄r.
Dijeljenje racionalnih brojeva (razlomaka) definišemo: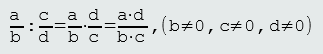
Skup racionalnih brojeva je uređen skup, odnosno za svaka dva racionalna broja r1 i r2 vrijedi:
a) r1=r2 ili
b) r1>r2 ili
c) r1<r2.
Racionalni brojevi se mogu prikazati i u obliku decimalnog broja, sa konačno ili beskonačno mnogo decimala.
1⁄2=0,5 3⁄4=0,75 5⁄6=0,8333333...