Teoreme o određenosti ravni
Teorema: Ravan je određena sa dvije prave koje se sijeku ili postoji jedna i samo jedna ravan koja sadrži dvije prave koje se sijeku.
Teorema: Ravan je određena sa jednom pravom i jednom tačkom van prave ili postoji jedna i samo jedna ravan koja sadrži datu pravu i datu tačku koja ne pripada datoj pravoj.
Teorema: Ravan je određena sa dvije različite paralelne prave ili postoji jedna i samo jedna ravan koja sadrži dvije paralelne prave.
Napomena: Ove teoreme ovdje nismo dokazivali, pokušajte to učiniti...
Definicija: Za dvije prave koje nemaju zajedničkih tačaka i leže u istoj ravni ili se poklapaju, kažemo da su paralelne.
Paralelne prave
Aksioma: Ako je u bilo kojoj ravni α data prava a i tačka A∉a, onda u tački A u ravni α postoji tačno jedna prava p koja je paralelna sa a.
Teorema: Ako su dvije prave a i b paralelne sa trećom pravom c, onda su one i međusobno paralelne.
a b, b c ⇒ a c
Napomena: Sve teoreme je potrebno dokazati; mi ćemo to u nekim slučajevima uraditi, a u drugim prepuštamo Vama...
Poluprava, Duž
Aksioma: Svaka tačka O na pravoj p dijeli skup tačaka prave na dva dijela tako da:
1. ako tačke A i B pripadaju raznim dijelovima, tada tačka O leži između A i B
2. ako tačke A i B pripadaju istom dijelu prave, tada se jedna od ovih tačaka nalazi između druge tačke i tačke O 

Definicija: Skup od dvije tačke prave (A i B) i svih tačaka koje se nalaze između te dvije tačke nazivamo duž (duž AB).
Tačke A i B se zovu krajevi duži, a sve ostale tačke se nazivaju unutrašnje tačke duži.
Poluravan, Poluprostor
Aksioma: Svaka prava p ravni dijeli tu ravan na dvije oblasti za koje vrijedi:
1. ako tačke A i B koje nisu na pravoj p pripadaju istoj oblasti, tada prava p ne siječe duž AB
2. ako tačke A i B koje nisu na pravoj p pripadaju raznim oblastima, tada prava p siječe duž AB

Ako pravu p priključimo poluravni, tada za poluravan kažemo da je zatvorena, u suprotnom je otvorena.
Kada posmatramo ravan, uočavamo da ona sve tačke prostora dijeli na dvije oblasti. Ako su dvije tačke u istoj oblasti, tada duž čiji su krajevi te tačke nema zajedničkih tačaka sa ravni. Ako su, međutim, tačke u raznim oblastima, duž čiji su krajevi te tačke ima jednu zajedničku tačku sa ravni.
Definicija: Jedna od oblasti na koju ravan dijeli prostor naziva se poluprostor.
Mjerenje duži, Mjerenje uglova
Odaberemo li jednu duž MN i sve druge duži upoređujemo s odabranom duži, onda svakoj duži možemo pridružiti po jedan pozitivan realan broj koji se zove dužina duži. Odabranoj duži pridružujemo broj 1 i ona se zove jedinična duž.
Duži mogu biti jednake i nejednake (jednake duži se na neki način mogu dovesti do potpunog poklapanja; ove duži imaju jednake dužine).
Dužina duži MN se takođe naziva i rastojanje tačaka M i N.
Tačka na duži MN koja ima jednako rastojanje od M i N zove se središte duži MN.
Posmatraćemo sada dvije poluprave p i q koje imaju zajednički početak O.
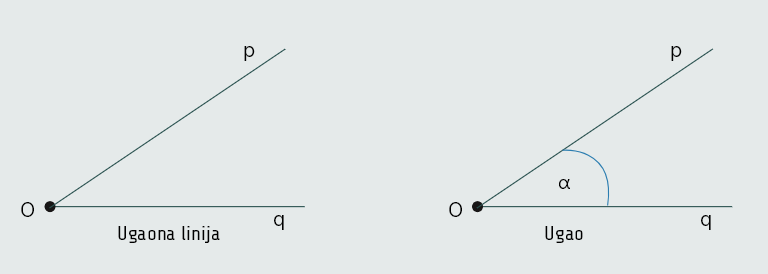
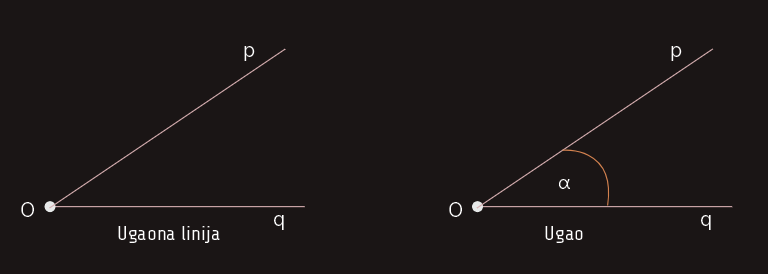
Unija polupravih Op i Oq naziva se ugaona linija. Ugaona linija dijeli ravan u kojoj se nalazi na dvije oblasti, i to unutrašnju i vanjsku. Svaku od ovih oblasti zajedno sa ugaonom linijom nazivamo ugao.
Zajednička početna tačka polupravih zove se vrh ugla, a poluprave se nazivaju kraci ugla.


Ako na pravoj a uzmemo bilo koju tačku O, tada ona određuje dvije suprotne poluprave čija je ugaona linija upravo prava a. Oblasti koje odgovaraju ovoj liniji su dvije poluravni čija je ivica a. Zbog ovoga poluravan sa odabranom tačkom na njenoj ivici možemo smatrati kao jedan specijalan ugao koji zovemo ravni ili ispruženi ugao.
Ako se dvije poluprave poklapaju, one onda ne dijele ravan na dva dijela i ugaona linija je tada zapravo samo jedna poluprava. Ovu polupravu možemo shvatiti kao nulti ili nula-ugao. Unutrašnjost nultog ugla je prazan skup, a oba kraka su ista poluprava.
Ako se dvije poluprave poklapaju, a unutrašnjost ugla je cijela ravan u kojoj se one nalaze, osim tačaka polupravih, onda takav ugao nazivamo puni ugao.
Susjedni uglovi su uglovi koji imaju zajednički jedan krak, pri čemu nemaju zajedničkih tačaka.
Ukoliko je unija dva susjedna ugla ravni ugao, tada uglove nazivamo naporedni uglovi.
Pravi ugao je specifičan slučaj i to kada je dati ugao jednak svom naporednom uglu.
Definicija: Ugao koji je jednak svom naporednom uglu naziva se pravi ugao. 

Definicija: Prava koja sadrži središte duži i koja je normalna na pravu koja sadrži tu duž naziva se simetrala duži.
Da bi smo mogli mjeriti uglove, potrebno je izabrati jedan ugao kao jedinični ugao, te sve druge uglove upoređivati sa ovim uglom. Ovakvim načinom se svakom uglu pridružuje jedan pozitivan realan broj koji pokazuje koliko se jediničnih uglova nalazi u posmatranom uglu. Za jedinični ugao uzima se: stepen, radijan i grad.
Stepen je devedeseti dio pravog ugla (oznaka 0), sadrži 60 minuta ('), a minuta sadrži 60 sekundi (").
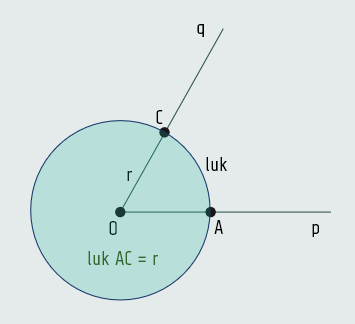
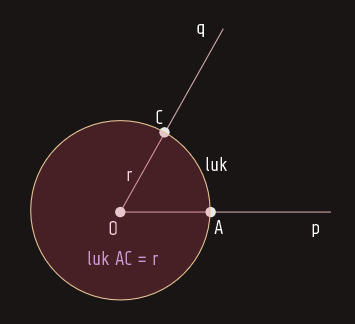
Radijan je onaj centralni ugao kod koga je pripadni luk jednak radijusu kružnice.
Puni ugao je 3600, a kako je dužina kružnice (obim kruga) jednak 2rπ, slijedi da punom uglu izraženom u radijanima odgovara 2π.
Ispruženi ugao ima 1800 ili π radijana, pravi ugao ima 900 ili π/2 radijana.
Grad je treća jedinica za mjerenje uglova; grad je stoti dio pravog ugla. Jedan grad ima 100 metričkih minuta ('), a jedna metrička minuta 100 metričkih sekundi (").
Definicija: Ako je mjera ugla manja od 900, za ugao kažemo da je oštar; ako je mjera ugla između 900 i 1800, ugao je tup.
Definicija: Za dva ugla čiji je zbir mjera 900, kažemo da su komplementni; a za dva ugla čiji je zbir mjera 1800, kažemo da su suplementni uglovi.
Definicija: Prava koja ugao dijeli na dva jednaka ugla naziva se simetrala ugla.