Radijan je onaj centralni ugao kod koga je pripadni luk jednak radijusu kružnice. Puni ugao je 360⁰, a kako je dužina kružnice (obim kruga) jednak 2rπ, slijedi da punom uglu izraženom u radijanima odgovara 2π. Ispruženi ugao ima 180⁰ ili π radijana, pravi ugao ima 90⁰ ili π/2 radijana.

Zadatak:
Izračunajmo dužinu luka kružnice radijusa 1cm ako je pripadni ugao 𝜔 = 32⁰18'48''.

Rješenje:

Minute i sekunde je prvo potrebno pretvoriti u stepene. Dakle, 1' = (1⁄60)⁰ i 1'' = (1⁄60)'.
Sada slijedi da je (π/180)·𝜔 = (3.14/180)·(32 + 18⁄60 + 48⁄360) = 0.56368
l(𝜔) = 0.56cm

Zadatak:
Na kružnici radijusa 1km uglu 𝜔 pripada luk dužine 653.2m. Koliki je ugao 𝜔?

Rješenje:

𝜔 = (180/π)·l = (180/π)·0.6532 = 37.445⁰
Pretvorimo dijelove stepena u minute i sekunde:
37.445⁰ = 37⁰ + (0.445 · 60)' = 37⁰ + 26.7' = 37⁰26' + (0.7 · 60)'' = 37⁰26'42''
𝜔 = 37⁰26'42''

Odnos perifernog i centralnog ugla kružnice

Ako uzmemo kružnicu radijusa r sa središtem u tački S, k(S,r), i na toj kružnici dvije tačke A i B, tada spojnica AB tačaka A i B se naziva tetiva kružnice, a prava kroz ove dvije tačke sekanta kružnice. Ta prava siječe kružnicu u tačkama A i B. Tačkama A i B određena su dva luka kružnice pri čemu svaki od tih lukova pripada tetivi AB. Dužina svakog od tih lukova je veća od dužine duži AB, jer vrijedi:
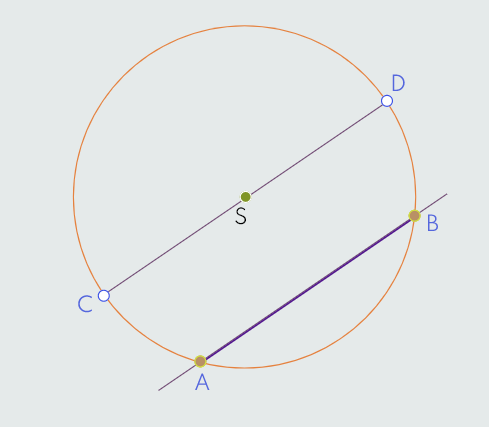
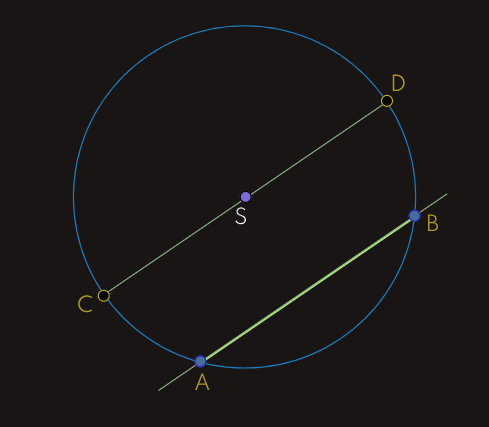
Od svih krivulja koje spajaju tačke A i B, duž AB ima najmanju dužinu. Očito je da tetiva koja sadrži središte kružnice ima najveću dužinu i ta se tetiva zove dijametar ili promjer kružnice, dok za krajnje tačke C i D kažemo da su dijametralne. Dužina dijametra je 2r, a kako je dužina kružnice O = 2rπ, dobivamo da je odnos dužine kružnice i dijametra O/2r neovisan o radijusu kružnice nego je ovisan o broju π = 3.14 (približna vrijednost) i on je isti za sve kružnice.

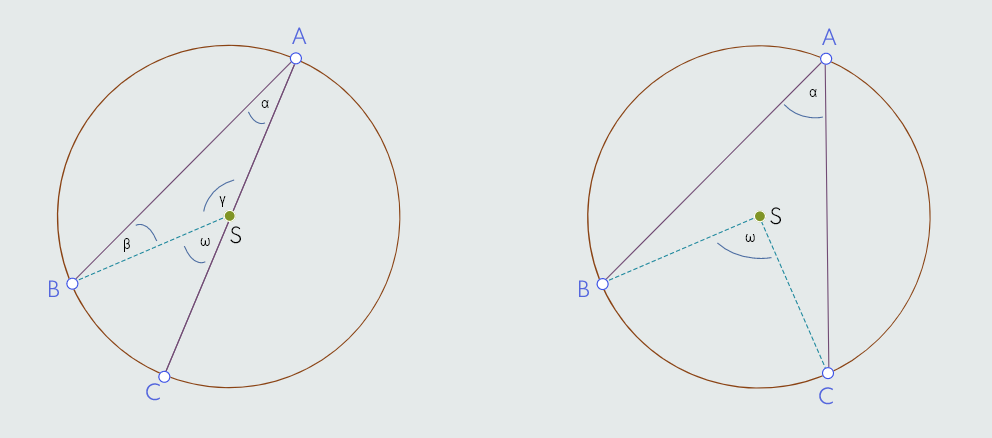
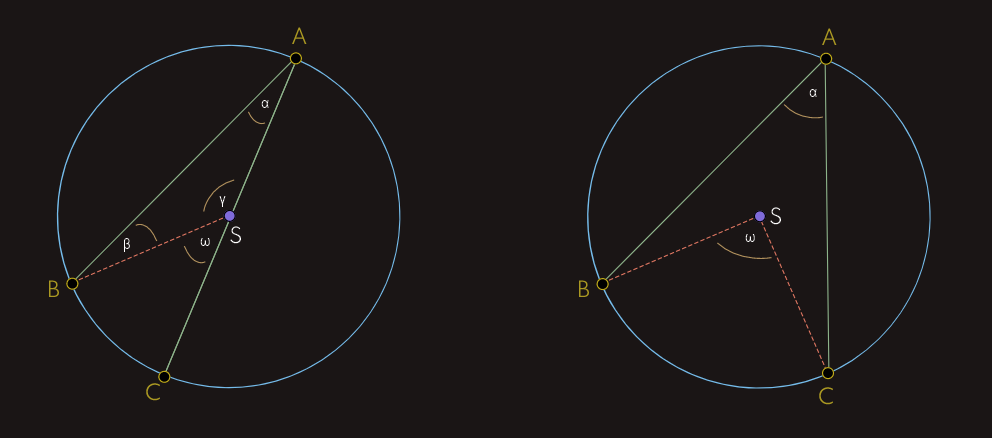
Tetiva kružnice dijeli (siječe) krug na dva dijela; svaki od tih dijelova zove se odsječak kruga. Dijametar kružnice dijeli krug na dva podudarna odsječka. Svaki od tih odsječaka zove se polukrug. Dijametralne tačke kružnice dijele kružnicu na dva podudarna luka; svaki od tih lukova zove se polukružnica. Gornja slika prikazuje kružnicu i dvije tetive AB i AC koje zatvaraju ugao α čiji je vrh na kružnici i zatvaraju ga tetive; taj se ugao zove periferni (obodni) ugao kružnice. Perifernom uglu α pripada središnji ugao 𝜔. U prvom slučaju, tetiva AC je dijametar.

Može se dokazati da je 𝜔 = 2α.
Ako uočimo trougao ABS, vidimo da su dvije stranice trougla jednake, imaju dužinu r, pa su i uglovi koji leže naspram tih stranica jednaki, tj. α = β, a kako je zbir uglova u trouglu 180⁰, to je α+β+γ = 180⁰, odnosno 2α = 180⁰-γ.
Vidljivo je na slici da je γ+ω = 180⁰, odakle je ω = 180⁰-γ, a to je ustvari 2α.

Na drugoj slici vidimo takođe periferni ugao α i središnji ugao ω koji pripada perifernom uglu, ali u ovom slučaju nijedna od tetiva nije dijametar.
Središte S kružnice je unutar perifernog ugla α.
Takođe je moguće dokazati i u ovom slučaju da je 𝜔 = 2α, tako što problem svodimo na dokaz u prvom slučaju...

Treći slučaj bi bio kada je središte S kružnice izvan perifernog ugla α, pri čemu su AB i AC takođe tetive, gdje nijedna nije dijametar, ali i tada je moguće izvesti dokaz da je ω = 2α.
Međutim, u ove dokaze se ovdje nećemo upuštati, ali ćemo navesti sljedeću teoremu...

Teorema: Periferni ugao jednak je polovini pripadnog centralnog ugla.
Pri tome je ugao α koji ima vrh na kružnici i kojeg zatvaraju dvije tetive te kružnice periferni ugao, a njemu pripadni centralni ugao ω je ugao koji ima vrh u središtu kružnice i isijeca isti luk na kružnici kao i ugao α.
Primjetno je da svakom perifernom uglu pripada samo jedan centralni ugao, ali da svakom centralnom uglu pripada beskonačno mnogo perifernih uglova. Svi ovi periferni uglovi su jednaki.

Posebno je zanimljiv slučaj kada centralni ugao ima 180⁰; tada periferni ugao leži nad dijametrom i ima 1⁄2 od 180⁰, tj. 90⁰, odnosno pravi je ugao, te na osnovu prethodne teoreme dobivamo novu teoremu (korolar, kao posljedica neke druge teoreme):
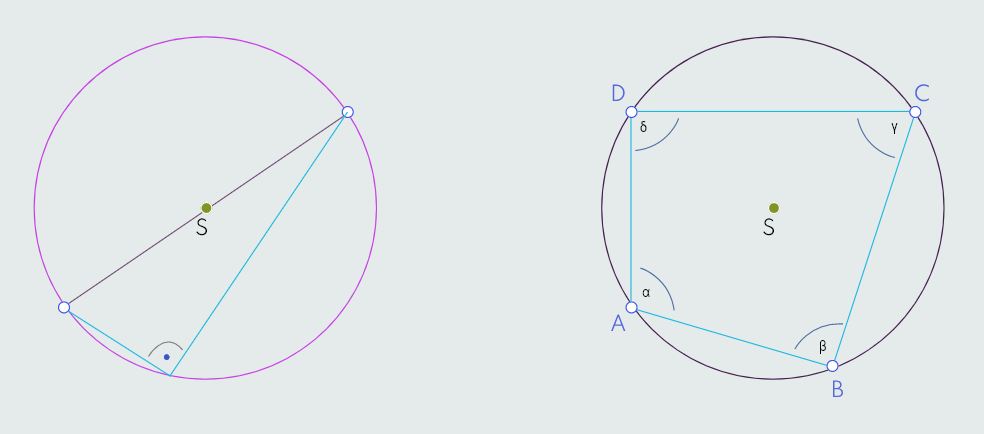
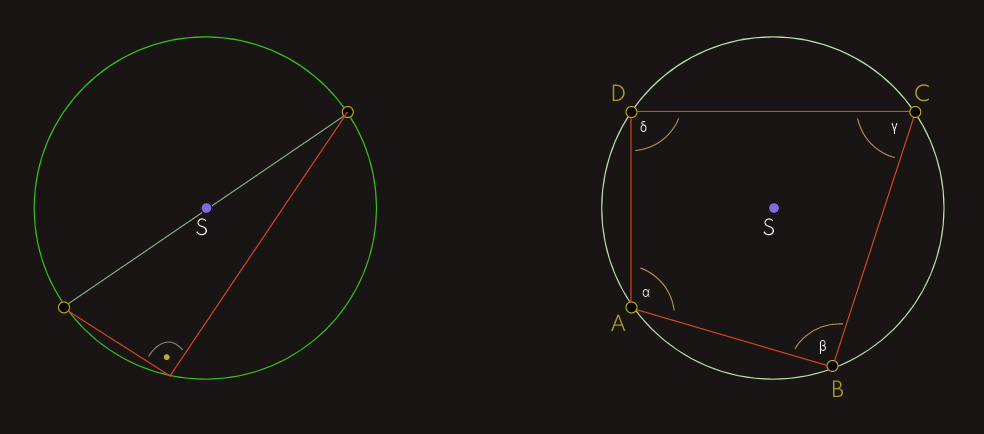
Periferni ugao nad dijametrom je pravi ugao. Ovaj rezultat je poznat kao Talesova teorema o perifernom uglu nad dijametrom. Odavde proizilazi da su ove tetive normalne.
Takođe, ako unutar kružnice nacrtamo četverougao ABCD, čiji vrhovi leže na kružnici i čije stranice čine tetive, tada se takav četverougao naziva tetivni četverougao u kojem je zbir naspramnih uglova jednak 180⁰, α+γ = β+δ = 180⁰.
Iz ove tvrdnje možemo zaključiti da vrijedi i obrnuta tvrdnja, odnosno ako za uglove konveksnog četverougla ABCD vrijedi α+γ = β+δ, onda je taj četverougao tetivni i može mu se opisati kružnica.

Pravilni poligoni

Ako su kod datog trougla sve tri stranice jednake, takav trougao zovemo jednakostraničan. U ovom trouglu su i uglovi jednaki, a kako je ukupan zbir uglova 180⁰, to znači da je svaki ugao jednak 60⁰. Iz ovih zaključaka proizilazi da su bilo koja dva jednakostranična trougla slična.
Jednakostraničan trougao i kvadrat su primjeri pravilnih poligona.
Konveksan poligon je pravilan ako su mu sve stranice jednake i svi (unutrašnji) uglovi jednaki.

Na osnovu kružnice radijusa 1 i pravilnog n-terougla upisanog u kružnicu, pomoću određene formule, moguće je izvesti broj π odnosno pokazati da je dužina polukružnice u ovom slučaju približno jednaka broju 3.14. Arhimed je dokazao da broj π leži između brojeva 3+10⁄71 i 3+1⁄7. Nizozemski matematičar Ludolf van Ceulen izračunao je broj π na 35 decimala, pa se ovaj broj često naziva i Ludolfov broj; slovenski matematičar Juraj Vega izračunao je broj π na 140 decimala kasnije, dok je danas ovaj broj izračunat na nekoliko miliona decimala!

Konstrukcija pravilnog 5-terougla omogućava konstrukciju pravilnog 10-terougla, pravilnog 20-terougla i tako dalje, općenito - pravilnog 5·2ⁿ-terougla za svaki prirodan broj n. Tako na primjer, ako su uzastopni vrhovi pravilnog 10-terougla: 1, 2, 3, 4, ..., 9, 10; onda su uzastopni vrhovi pravilnog peterougla: 1, 3, 5, 7, 9.

Pojam zlatni rez uveo je Leonardo da Vinci (1452-1519), a otkriće pentagrama dugujemo Pitagorejcima. Ovim otkrićem, oni su geometrijskim putem srušili svoju dogmu (mit), prema kojoj su bilo koje dvije duži samjerljive i još i više - da je sve na svijetu određeno omjerima prirodnih brojeva. Došlo se, dakle, do otkrića iracionalih brojeva, jednog od najvažnijih otkrića u matematici. Kritičnost dokazivanja je povišena i obogaćena, razum se uzdigao iznad intuicije, ali će ipak biti potrebno 2000 godina nakon otkrića iracionalnih brojeva da se u potpunosti shvate realni brojevi, i to u 19. stoljeću.