Kinetička energija

Energiju koju tijelo ima zbog svoga kretanja nazivamo kinetičkom energijom, E_k [džul, J].
Ona je proporcionalna masi tijela m i kvadratu njegove brzine v: \(E_k = \frac{1}{2}mv^2\).

Od dvaju tijela jednakih masa, veću kinetičku energiju ima ono tijelo koje se kreće većom brzinom. A takođe, od dvaju tijela koja se kreću jednakom brzinom, veću kinetičku energiju ima tijelo veće mase. Dakle, kinetička energija ovisi o masi tijela i o brzini kojom se tijelo kreće.

Kad tijelo ubrzava i brzina mu se povećava, kinetička energija tijela se povećava. Npr. kad automobil prestiže drugi automobil na cesti, brzina mu se povećava, a time se povećava i njegova kinetička energija. Kad tijelo usporava i brzina mu se smanjuje, kinetička energija takođe mu se smanjuje. Npr. kad automobil koči, brzina mu se smanjuje, a time se smanjuje i njegova kinetička energija. Kad se tijelo kreće stalnom brzinom, brzina mu se ne mijenja, pa mu je i kinetička energija stalna, npr. kad automobil vozi na autocesti stalnom brzinom od 130 km/h.

Svako tijelo koje se kreće ima kinetičku energiju. Rijeka se kreće i zbog toga ima energiju, vjetar je kretanje zraka, pa i on ima energiju, ptica takođe se kreće, ima energiju itd.

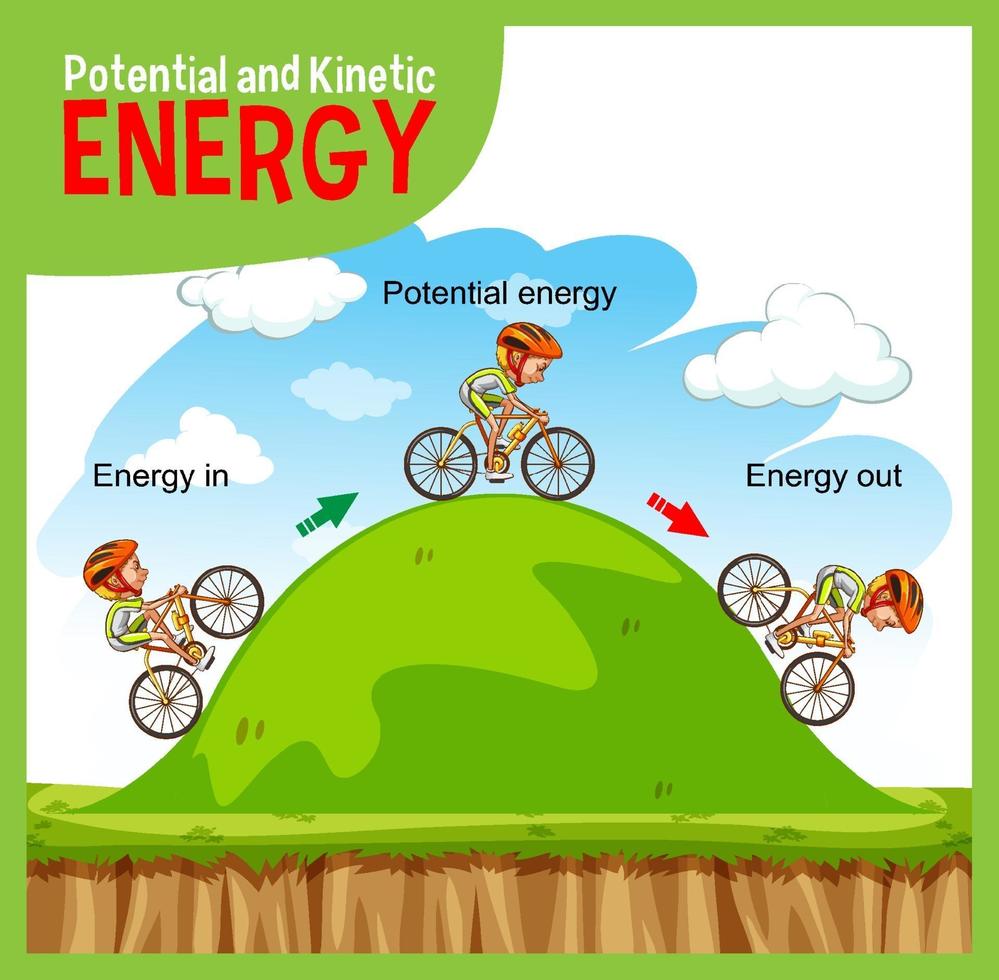
Gravitacijska potencijalna energija

Tijelo ima potencijalnu energiju jer je pod djelovanjem sile (sile teže, magnetske sile, elastične sile itd). Gravitacijsku potencijalnu energiju imaju tijela zbog djelovanja sile teže; tijela imaju ovu energiju zbog svog položaja u odnosu na površinu Zemlje, E_gp [džul, J].

Gravitacijska potencijalna energija ovisi o visini na kojoj se tijelo nalazi, E_gp ˜ h. Na primjer, voda u akumulacijskom jezeru ima veliku gravitacijsku potencijalnu energiju zbog visine na kojoj se nalazi. Takođe je gravitacijska potencijalna energija srazmjerna masi tijela, E_gp ˜ m. Dakle, tijelo mase m koje se nalazi na visini h iznad površine Zemlje ima gravitacijsku potencijalnu energiju: \(E_{gp} = mgh\), pri čemu je \(g = 10 \frac{N}{kg}\).

Pri određivanju gravitacijske potencijalne energije potrebno je odrediti početnu razinu u odnosu na koju računamo gravitacijsku potencijalnu energiju tijela. Tri kuglice jednakih masa nalaze se na različitim visinama u odnosu na tlo; najmanju gravitacijsku potencijalnu energiju ima kuglica C.

Elastična potencijalna energija

Kada elastična tijela zbog djelovanja vanjske sile promijene oblik, ona imaju elastičnu potencijalnu energiju. Što su promjene oblika elastičnog tijela veće, to je elastična potencijalna energija veća. Tijela pod uticajem vanjske sile mijenjaju oblik, ali samo se elastična tijela vraćaju u prvobitni oblik. Takva je npr. košarkaška lopta koja prilikom udara od pod nakratko promijeni oblik te se zbog djelovanja elastične sile odbija od poda i vraća u prvobitni oblik, zatim gumica za kosu, opruga, luk i strijela itd. Elastična energija pohranjena je u luku i savijanjem luka prenosi se na strijelu, te strijela dobiva kinetičku energiju.

Dakle, elastična potencijalna energija je energija pohranjena u elastičnim tijelima kojima je oblik promijenjen zbog djelovanja neke vanjske sile, E_ep [džul, J].

Kad elastičnim tijelima promijenimo oblik, ona se tome opiru elastičnom silom. Ako prestane djelovanje vanjske sile, elastična sila vraća tijela u njihov prvobitni oblik. Elastičnu silu računamo izrazom \(F_{el} = -kΔl\), pri čemu je k konstanta opruge, a Δl produženje opruge. Minus u formuli označava smjer elastične sile, koji je suprotne orijentacije od djelovanja sile koja rasteže ili pritišće oprugu.

Elastičnu potencijalnu energiju računamo izrazom: \(E_{ep} = \frac{k(Δl)^2}{2}\).

Pretvorbe energije

Energija oko nas nalazi se u različitim oblicima. Energija se može pohraniti u tijelima, može prijeći s tijela na tijelo i pretvoriti se iz jednog oblika u drugi.
Tako na primjer na vrhu staze za skateboard dječak ima najveću gravitacijsku potencijalnu energiju jer se nalazi na najvišoj visini. Spuštanjem niz stazu njegova gravitacijska potencijalna energija pretvara se u kinetičku energiju. Njegova kinetička energija najveća je na dnu staze i tu je najbrži, a gravitacijska potencijalna energija u toj mu je tački najmanja. Dok se ponovno penje uz stazu, brzina mu se smanjuje, a time se smanjuje i kinetička energija. Gravitacijska potencijalna energija mu se povećava. Zbog trenja točkova o podlogu te skateboarda i dječaka o čestice zraka dio kinetičke energije pretvara se u energiju zbog koje su se točkovi, podloga i okolina zagrijali.
Drugi primjer na trampolini uključuje gravitacijsku potencijalnu energiju, kinetičku energiju i elastičnu potencijalnu energiju. Na početku igre dječak skače na trampolinu s neke visine i ima gravitacijsku potencijalnu energiju. Kad je skočio, njegova gravitacijska potencijalna energija pretvorila se u njegovu kinetičku energiju. Kad dječak doskoči na trampolini, njegova kinetička energija pretvara se u elastičnu potencijalnu energiju trampoline te se platno sprave rasteže. Sad je u platnu pohranjena elastična potencijalna energija. Platno se želi vratiti u prvobitni oblik te predaje dječaku energiju koja postupno prelazi u njegovu kinetičku energiju, koja se zatim pretvara u gravitacijsku potencijalnu energiju. Dječak nakon toga ponovno pada na trampolinu i tako sve dok ima dovoljno energije za to da odskoči od trampoline, jer se dio energije predaje okolini, trampolini i ostaloj djeci za zagrijavanje.

Dakle, ukupna energija je nepromijenjena, tj. sačuvana. Energija ne može nestati ili nastati ni iz čega, ona može prelaziti s tijela na tijelo, može prelaziti iz jednog oblika u drugi te se može pohraniti. To opisuje jedan od temeljnih zakona u prirodi, koji se zove zakon o očuvanju energije.

Kinetičku energiju, gravitacijsku potencijalnu energiju i elastičnu potencijalnu energiju jednim imenom nazivamo mehanička energija.
Zakon očuvanja mehaničke energije možemo iskazati izrazom E_u = E_k + E_gp + E_ep, pri čemu je ukupna energija jednaka zbiru kinetičke energije i potencijalnih energija. Taj zakon vrijedi kad nema pretvaranja mehaničke energije u druge oblike; što vrijedi za izolirane sisteme koji ne izmjenjuju energiju s okolinom. Primjenjujemo ga u primjerima u kojima zanemarujemo rad potreban za svladavanje sile trenja, jer je on vrlo malen.

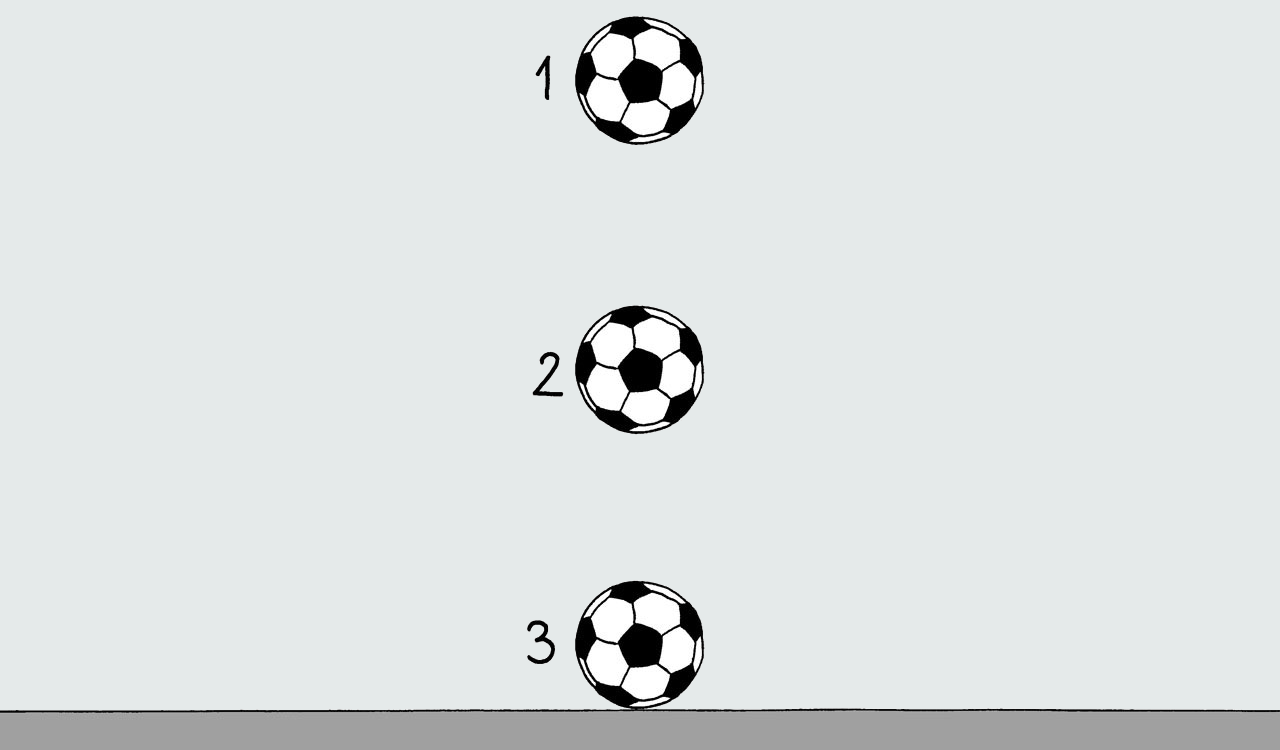
Lopta mase m koja se nalazi na visini h ima određenu gravitacijsku potencijalnu energiju. U položaju 1 gravitacijsku potencijalnu energiju računamo pomoću formule E_gp = mgh. U tom položaju lopta nema kinetičku energiju jer miruje i nema brzinu.
Ukupna energija lopte jednaka je zbiru kinetičke i potencijalne energije.
E_u = E_gp1 + E_k1
E_k1 = 0
E_u = E_gp1
Kad ispustimo loptu iz ruke, ona pada te se njezina gravitacijska potencijalna energija smanjuje, a kinetička energija raste. Zbir kinetičke i gravitacijske potencijalne energije u bilo kojem slučaju je stalan.
E_u = E_k2 + E_gp2
Trenutak prije udara gravitacijska potencijalna energija koju je lopta imala na visini potpuno se pretvorila u kinetičku energiju lopte.
E_u = E_k3 + E_gp3
E_gp3 = 0
E_u = E_k3

Zakon očuvanja energije opisuje da je energija očuvana, da prelazi s jednog tijela na drugo i iz jednog oblika u drugi, da ne nastaje i ne nestaje.