Zadatak:
Ako neki broj pomnožimo sa 9 i proizvodu dodamo 4, rezultat će biti veći od 35. Potrebno je pronaći najmanji cijeli broj za koji ovo vrijedi?
Rješenje:
Dakle, postavljajući nejednačinu, imamo:
9·x + 4 > 35
9x > 31
x > 31/9
x > 3,44
Najmanji cijeli broj za koji ova nejednačina vrijedi je broj 4.
Ako bismo, međutim, rješenje zaokružili na cijeli broj, dobili bismo broj 3, koji ne zadovoljava postavljeni uslov:
9·3 + 4 = 31 što nije veće od 35.
Geometrija ravni
Geometrija je nastala iz praktičnih potreba čovjeka da posmatra objekte oko sebe, proučava njihove osobine, uzajamne odnose i sl. Svi ovi objekti ispunjavaju prostor oko nas; taj prostor zovemo realni prostor, a apstrakcijom svih osobina ovih objekata nastaju geometrijska tijela, odnosno geometrijske figure. Ove figure ispunjavaju prostor koji nazivamo geometrijski prostor. Geometrijski prostor je, dakle, apstraktan prostor čije su osobine određene unaprijed datim pravilima - aksiomama uz nastojanje da se osobine geometrijskog prostora što više približe osobinama realnog prostora. Geometrijski prostor ispunjen je figurama; svaka figura sastoji se od tačaka. Dio elementarne geometrije u kojem se proučavaju osobine geometrijskih figura jedne ravni naziva se planimetrija, dok je za geometrijske figure koje nisu u istoj ravni - stereometrija.
Tačka, prava i ravan
U geometriji se kao osnovni pojmovi uzimaju tačka, prava i ravan; uz ove pojmove se još kao osnovni uzimaju skup, elemenat skupa, elemenat pripada skupu. Sve ostale pojmove moramo definisati. Rečenice kojima se objašnjavaju nepoznati pojmovi nazivaju se definicije. Svaki pojam, osim osnovnog, ima svoju definiciju. Definicija je ispravna ako se pojam definiše samo pomoću pojmova koji su prethodno definisani ili su osnovni (nepoznate pojmove nemoguće je objašnjavati nepoznatim, ali i poznati pojmovi morali su biti objašnjeni pomoću nekih drugih poznatih pojmova, ovi pomoću drugih itd., pri čemu se i dolazi do zaključka da se svi pojmovi ne mogu definisati, zato se određeni pojmovi uzimaju kao poznati bez definisanja, te se svi ostali definišu pomoću osnovnih i onih pojmova koji su definisani na osnovu njih). Ostali pojmovi se nazivaju izvedeni.
Definicija 1: Neprazan skup tačaka nazivamo geometrijska figura.
Definicija 2: Iskaz koji smatramo istinitim bez obrazlaganja nazivamo aksioma.
Definicija 3: Iskaz čiju istinitost obrazlažemo na osnovu aksioma nazivamo teorema.
Definicija 4: Postupak obrazlaganja istinitosti neke teoreme naziva se dokaz.
Ovdje ćemo kazati da je prava potpuno određena dvjema različitim tačkama (aksioma); tačke koje pripadaju jednoj istoj pravoj nazivaju se kolinearne tačke (definicija), dok se one koje to nisu nazivaju nekolinearne (definicija). Postoje tri tačke koje nisu na istoj pravoj (aksioma).
Svake tri nekolinearne tačke pripadaju jednoj i samo jednoj ravni (aksioma). Svaka ravan sadrži barem tri nekolinearne tačke (aksioma).
Ove tačke koje pripadaju jednoj istoj ravni nazivaju se komplanarne, dok su one koje to nisu nekomplanarne.
Postoje četiri tačke koje nisu u jednoj istoj ravni.
Teorema: Dvije različite prave mogu imati najviše jednu zajedničku tačku.
Dokaz: Pretpostavimo da prave mogu imati dvije zajedničke tačke A i B. S obzirom da po prethodnoj aksiomi, gdje je prava potpuno određena dvjema različitim tačkama, odnosno da dvije različite tačke uvijek pripadaju jednoj i samo jednoj pravoj - ovdje bi po našoj pretpostavci tačkama A i B prolazile prave a i b koje ne bi bile različite, nego bi se podudarale. Teorema, međutim, govori da se radi o različitim pravama, tako da ostaje da one imaju jednu ili nemaju nijednu zajedničku tačku, dakle najviše jednu.
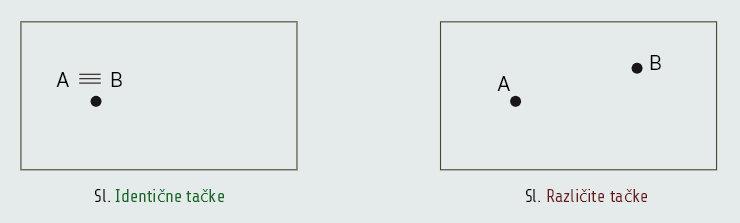
Međusobni položaj dvije tačke
Jedina dva moguća slučaja uzajamnog odnosa dviju tačaka su:
1. dvije tačke mogu da se poklapaju
2. dvije tačke mogu da budu različite

Međusobni položaj tačke i prave
Za tačku M i pravu p postoje dva uzajamna položaja:
1. tačka M pripada pravoj p (M ∈ p)
2. tačka M ne pripada pravoj p (M ∉ p)


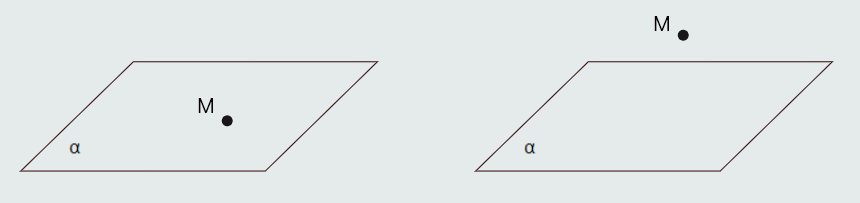
Međusobni položaj tačke i ravni
Tačka M i ravan α mogu imati sljedeće odnose:
1. tačka M pripada ravni α (M ∈ α)
2. tačka M ne pripada ravni α (M ∉ α)

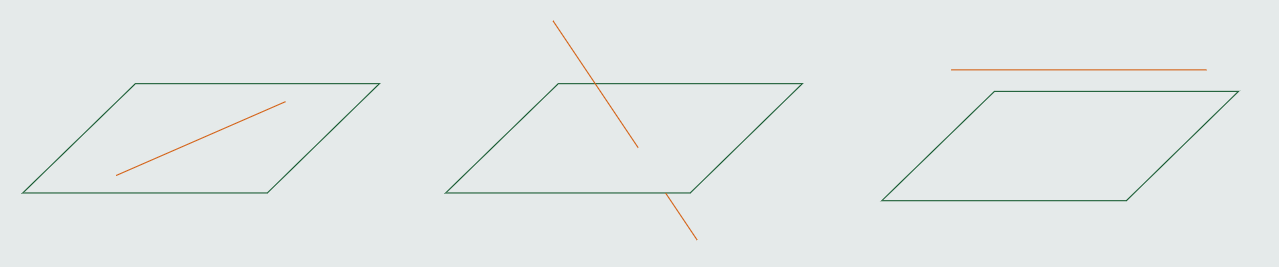
Međusobni položaj prave i ravni
Prava i ravan mogu imati tri različita međusobna odnosa:
1. prava leži u ravni; tada su sve tačke prave ujedno i tačke ravni.
2. prava i ravan imaju samo jednu zajedničku tačku; tj. prava prodire ravan u toj tački, prava i ravan se sijeku.
3. prava i ravan nemaju zajedničkih tačaka; prava je paralelna ravni.

Međusobni položaj dvije prave
Za dvije prave a i b postoje sljedeći uzajamni položaji:
1. prave imaju samo jednu zajedničku tačku; u ovom slučaju kažemo da se prave sijeku.
2. prave imaju barem dvije zajedničke tačke; kada kažemo da se prave poklapaju.
Napomenimo da se prave koje se poklapaju mogu smatrati i paralelnim pravima; tada paralelnost pravih posmatramo u užem i širem smislu.
3. dvije prave leže u jednoj ravni i nemaju zajedničkih tačaka; tada su one paralelne.
4. prave još mogu da ne leže u istoj ravni i da nemaju zajedničkih tačaka; takve prave nazivamo mimoilazne prave.
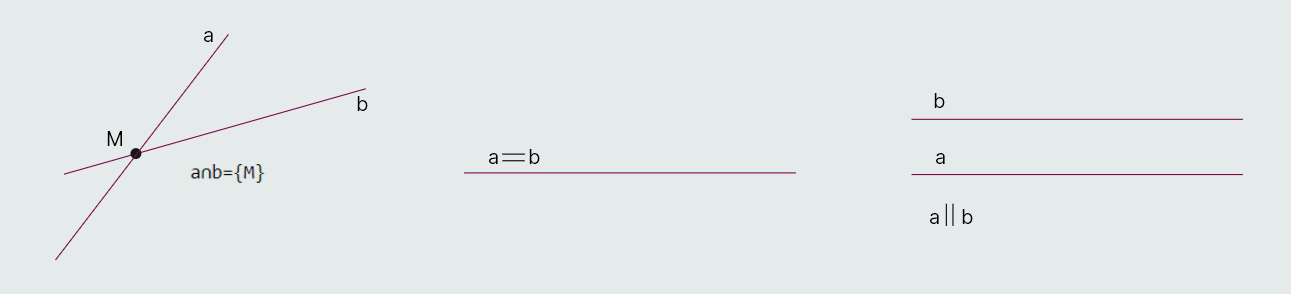
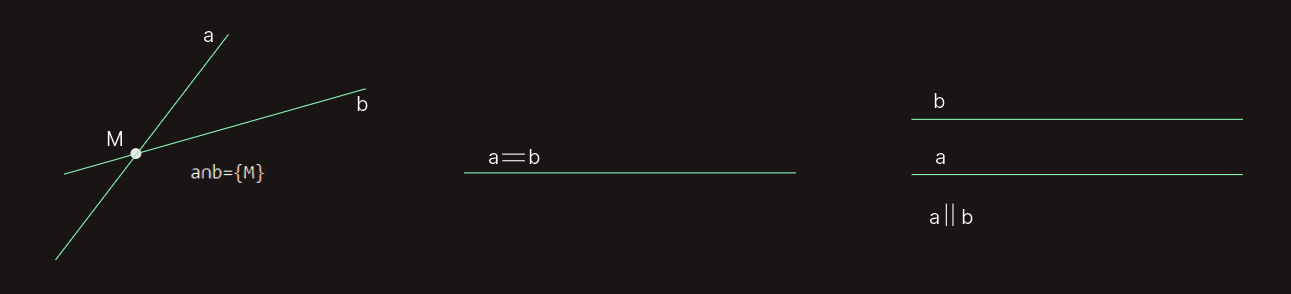
Međusobni položaj dvije ravni
Dvije ravni α i β imaju sljedeće uzajamne položaje:
1. ravni α i β imaju tri zajedničke nekolinearne tačke; tada se one poklapaju α=β ili α≡β.
2. ravni imaju zajedničku pravu p; tada kažemo da se one sijeku po pravoj p (α∩β=p).
3. ravni su u položaju takvom da nemaju nijednu zajedničku tačku; tada su paralelne (α β).