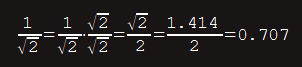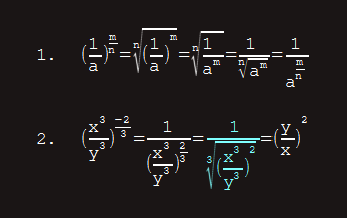Teorema: Ako su a≠0 i b≠0 realni brojevi, onda za svaki cijeli broj m vrijedi:
(a·b)m = am·bm
(a/b)m = am/bm,
što predstavlja pravilo za množenje i pravilo za dijeljenje stepena različitih baza, respektivno.
Drugi korijen iz pozitivnog realnog broja
U skupu racionalnih brojeva ne postoji broj x takav da je x2 = 2. Ova jednačina ima rješenje tek u skupu realnih brojeva i ono iznosi √2. Međutim, - √2 je takođe rješenje date jednačine.
Na isti način i jednačina x2 = 3 ima rješenja √3 i - √3 u skupu R.
Pozitivan realan broj x za koji je x2 = a zovemo drugi (kvadratni) korijen iz a i označavamo sa √a.
Drugo rješenje jednačine x2 = a, dakle je - √a. Ako se podsjetimo da je za svaki realan broj x, x2 ≥ 0, zaključujemo da jednačina x2 = -1 nema rješenja u skupu R.
Zbog toga se skup realnih brojeva proširuje do skupa kompleksnih brojeva u kojem i ovakva jednačina ima rješenje.
Teorema: Ako su a i b pozitivni realni brojevi onda je √(a·b) = √a·√b.
Teorema: Ako su a i b pozitivni realni brojevi onda je √(a/b) = √a/√b.
Racionalizacija nazivnika je proces u kojem se prilikom rješavanja zadatka oslobađamo (rješavamo) korijena u nazivniku razlomka.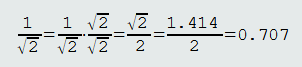 
Korijeni
Ako je a pozitivan realan broj, onda jednačina x3 = a ima najviše jedno rješenje u skupu realnih brojeva. Naravno, ovdje u obzir dolaze samo pozitivni brojevi x, jer je za x<0 i x3<0.
Ako je a pozitivan realan broj, onda jednačina x4 = a ima najviše jedno rješenje x>0 u skupu realnih brojeva.
Zapravo, ovdje smo naveli dva primjera, ali se stvari mogu generalizovati kroz sljedeću teoremu, ne upuštajući se u detaljniju analizu...
Teorema: Za svaki realan broj a>0 i za svaki prirodni broj n postoji jedinstven realan broj x>0 takav da je xn = a. Ovaj broj označavamo sa n√a (n-ti korijen iz a).
Teorema: Ako su a i b pozitivni realni brojevi, onda za svaki prirodni broj n vrijedi:
n√(a·b) = n√a · n√b
n√(a/b) = n√a / n√b
Takođe navodimo sljedeću teoremu:
Teorema: Ako je a pozitivan realan broj, onda za sve prirodne brojeve n, m i p vrijedi:
n√am = np√amp → proširivanje/skraćivanje korijena,
(n√a)p = n√ap → stepenovanje korijena, odnosno korijen stepena,
n√m√a = nm√a → korjenovanje korijena.
Napomena: U korijenu n√a, a zovemo radikand, a n eksponent korijena. Sam proces vađenja (uzimanja, određivanja) korijena iz broja nazivamo korjenovanje ili radiciranje.
Stepen racionalnog eksponenta
Ako je r=m/n > 0 (m,n ∈ N) racionalan broj, onda definišemo:
ar = am/n = n√am.
Dakle, a1/3 = 3√a, itd.
Ako je racionalan broj r negativan, definišemo:
ar = 1/a-r.
Tako je npr. a-2⁄5 = 1/a2⁄5 = 1/5√a2.
Primjer: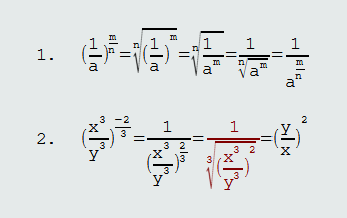 
Kružnica, krug i pravilni poligoni
Dužina kružnog luka i površina isječka kruga
Ako sa duži AB, prikazanoj na donjoj slici, uklonimo tačku P, onda se ta duž dijeli na dva dijela. Ukoliko isti princip primjenimo na kružnicu, takođe na donjoj slici, ona se ne dijeli, tj. kružnica ostaje u jednom dijelu, ostaje povezana. Da bismo kružnicu podijelili na dva dijela, potrebno je ukloniti dvije različite tačke A i B na kružnici.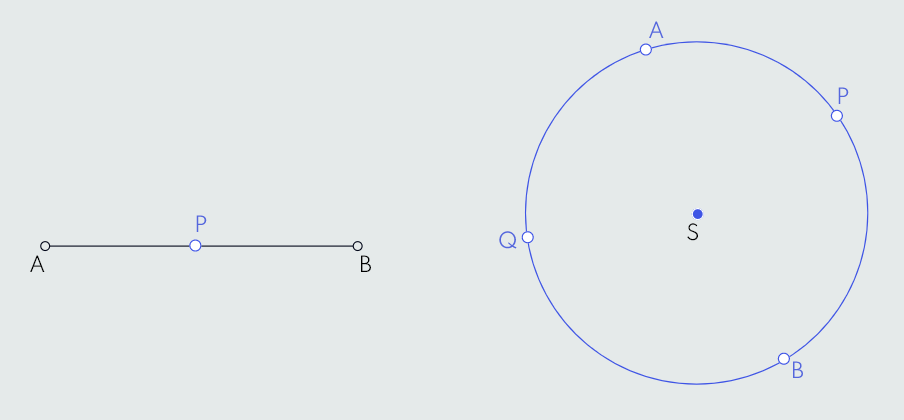 
Svaki od dobijenih podskupova kružnice zove se luk kružnice. Tačke A i B su rubovi ili krajnje tačke dobijenih lukova. Da bismo pobliže odredili ove lukove, uzimamo još dvije tačke P i Q na kružnici, tako da govorimo o luku APB ili BPA, odnosno luku AQB ili BQA.
Sljedeća slika prikazuje kružnicu radijusa r sa središtem u tački S, u kojoj se nalazi vrh ugla 𝜔, koji iz kruga i na kružnici isijeca dijelove koje zovemo kružni isječak i luk kružnice, respektivno.
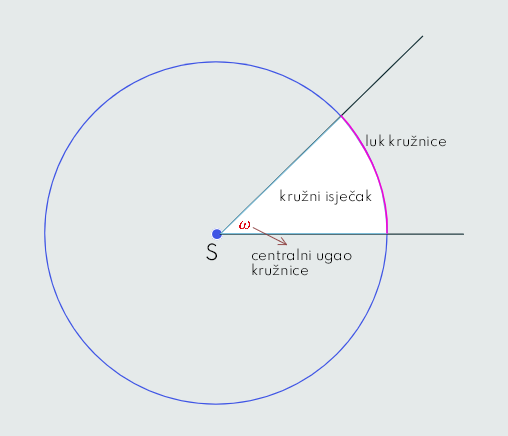
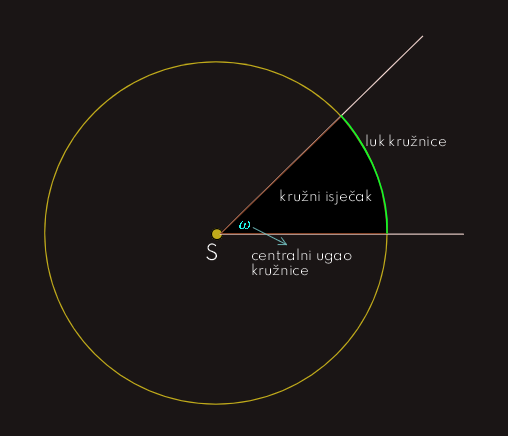
Sa P(𝜔) označit' ćemo površinu kružnog isječka, a sa l(𝜔) dužinu luka kružnice što ga isijeca ugao 𝜔. Sada nas zanimaju formule za izračunavanje P(𝜔) i l(𝜔) pomoću ugla 𝜔 i radijusa kružnice r.
Podsjetit' ćemo se da je obim kruga radijusa r jednak 2rπ, a površina je jednaka r2π, pri čemu je π približno jednak 3.14, isti za sve kružnice. Na osnovu prethodnog, možemo zaključiti da pravi ugao (900) isijeca 1⁄4 kruga i 1⁄4 kružnice, pa je P(900) = 1⁄4 · r2π, kao i l(900) = 1⁄4 · 2rπ.
Sada je lako izračunati koliki isječak i luk isijeca devedeseti dio pravog ugla, tj. ugao od 10.
P(10) = 1⁄90 P(900) = 1⁄90 · 1⁄4 · r2π = 1⁄360 · r2π
l(10) = 1⁄90 l(900) = 1⁄90 · 1⁄4 · 2rπ = 1⁄360 · 2rπ
Zaključujemo da je kružni isječak i luk kružnice koji isijeca ugao od 𝜔 stepeni, upravo 𝜔 puta veći od onog isječka i luka koji isijeca ugao od 10.
P(𝜔) = 𝜔 · 1⁄360 · r2π
l(𝜔) = 𝜔 · 1⁄360 · 2rπ = 𝜔 · 1⁄180 · rπ
Uglove mjerimo u stepenima. Pravi ugao ima 90 stepeni, jedan stepen ima 60 minuta, 1 minuta 60 sekundi; sekunde se dijele prema decimalnom sistemu na deset, stotinu, itd.
Primjer:
α = 22040'18.08'' → ugao α ima 22 stepena, 40 minuta, 18 sekundi i 8 stotina sekunde.
Takođe, uglove možemo mjeriti i na drugačiji način; umjesto da pravi ugao dijelimo na 90 jednakih dijelova, možemo ga podijeliti na 100 jednakih dijelova ili sl. Pokazuje se, međutim, da je uglove najprirodnije mjeriti pomoću radijana.