Mnogougaona linija, Trougaona linija
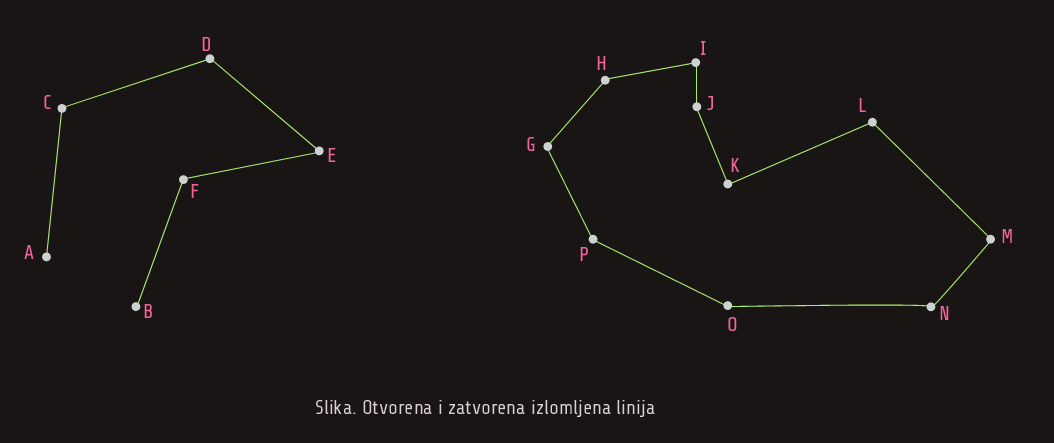
Za dvije duži kažemo da su nadovezane ako ne pripadaju istoj pravoj i imaju jednu zajedničku tačku. Unija nadovezanih duži predstavlja izlomljenu liniju; ona može biti otvorena i zatvorena. 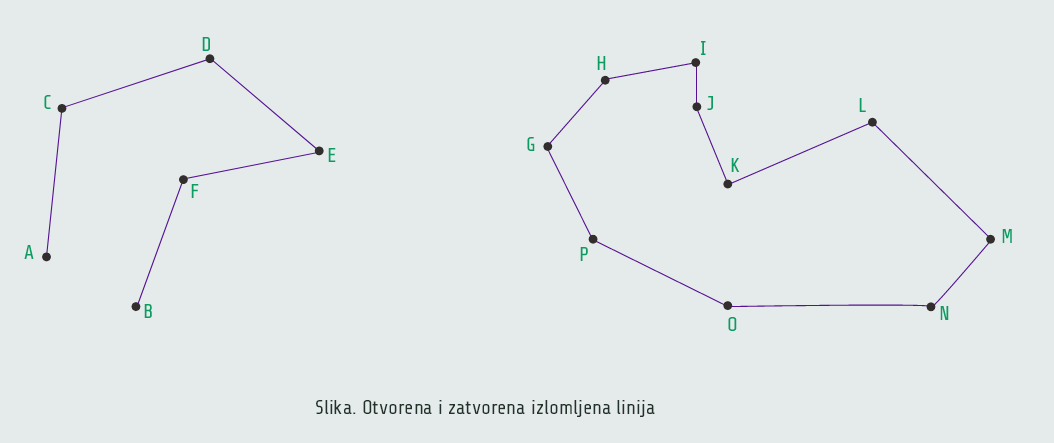
Mnogougao, Trougao
Dio ravni koji je zagrađen mnogougaonom linijom naziva se unutrašnja oblast te linije, dok je druga oblast mnogougaone linije vanjska oblast.
Definicija: Unija mnogougaone linije i njene unutrašnje oblasti naziva se mnogougao. Duži koje sačinjavaju mnogougaonu liniju zovu se stranice mnogougla, a krajnje tačke su vrhovi mnogougla.
Duži čiji su krajevi dva nesusjedna vrha mnogougla zovu se dijagonale mnogougla.
Mnogougao koji ima sve jednake stranice i sve jednake unutrašnje uglove naziva se pravilan mnogougao.
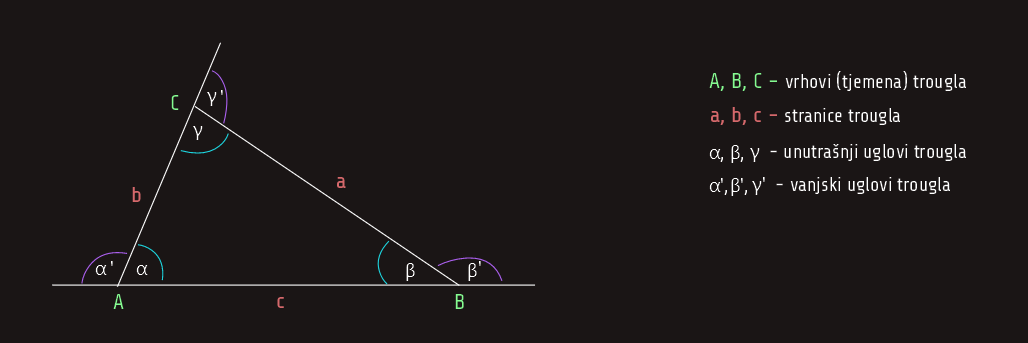
Definicija: Mnogougao sa tri stranice naziva se trougao. 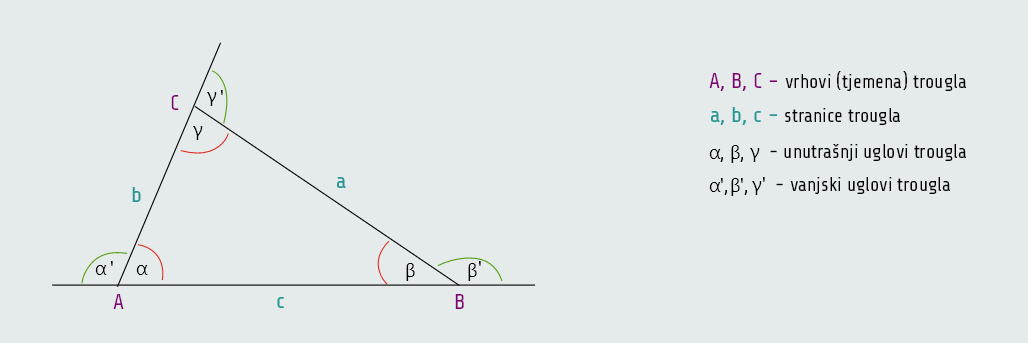
Definicija: Visina trougla, spuštena iz datog vrha trougla, je dio normale povučene iz tog vrha na pravu koja sadrži suprotnu stranicu trougla. Sve tri visine trougla sijeku se u istoj tački koja se zove ortocentar. 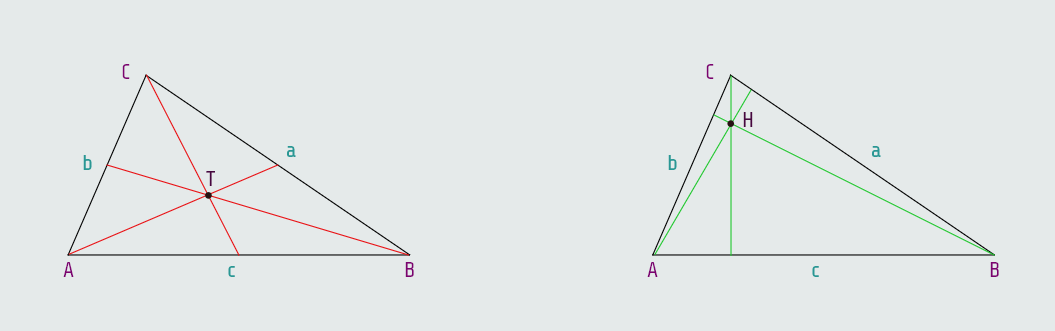
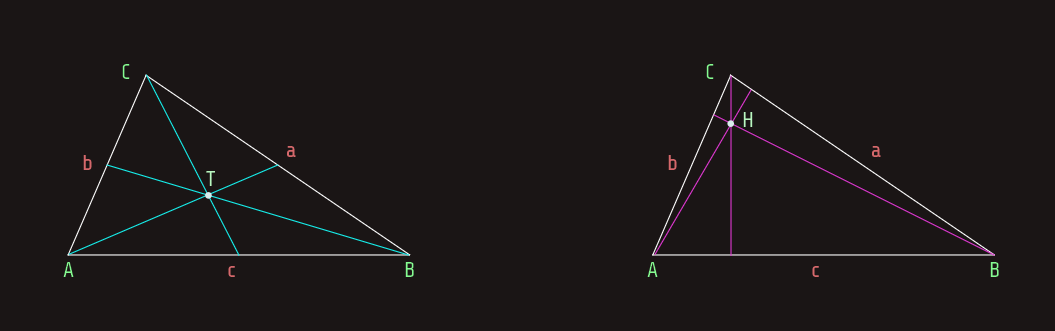
Podudarnost trouglova
Neka imamo dva trougla: ABC i A'B'C'; zamislimo da trougao ABC možemo pomjerati u ravni, pomicati, okretati, pa i prevrnuti. Ako se ovakvim pomjeranjem trougao ABC može dovesti u položaj da se poklopi sa trouglom A'B'C', onda kažemo da su trouglovi podudarni ili kongruentni.
Definicija: Dva trougla su podudarni ako je svaka stranica jednog trougla jednaka odogovarajućoj stranici drugog i ako je svaki ugao jednog trougla jednak odgovarajućem uglu drugog.
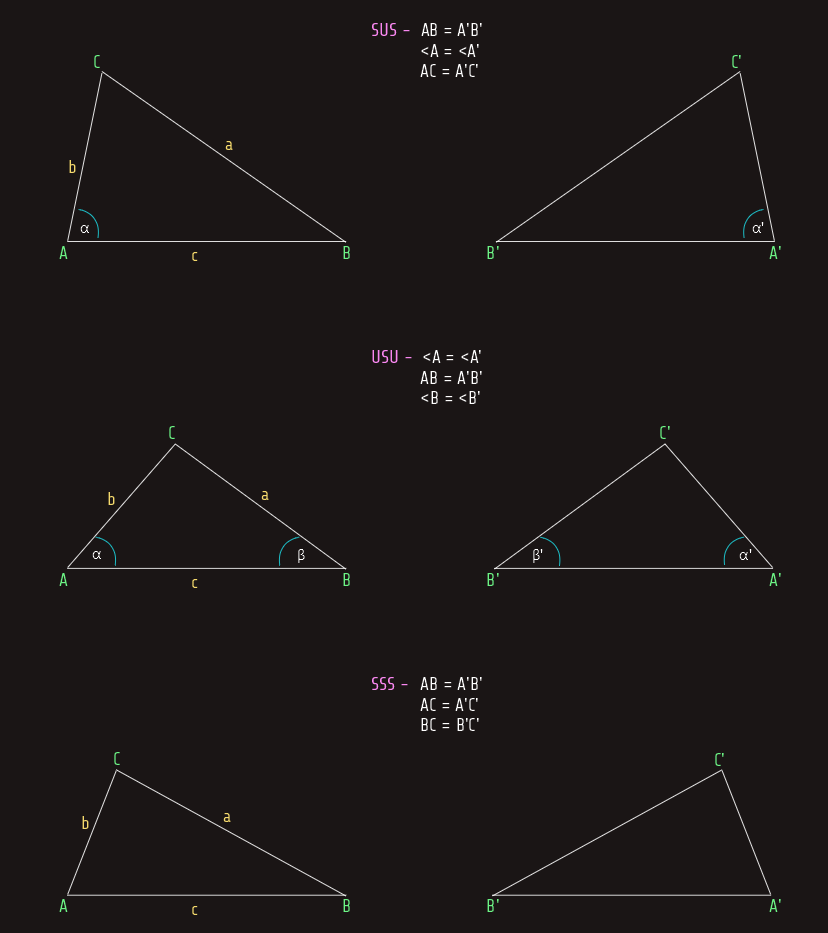
Nije potrebno provjeravati sve uslove, odnosno ovih 6 uslova da bismo utvrdili podudarnost trouglova; o ovome govore sljedeći aksiomi:
· SUS (stranica-ugao-stranica)
· USU (ugao-stranica-ugao)
· SSS (stranica-stranica-stranica)
· SSU (stranica-stranica-ugao)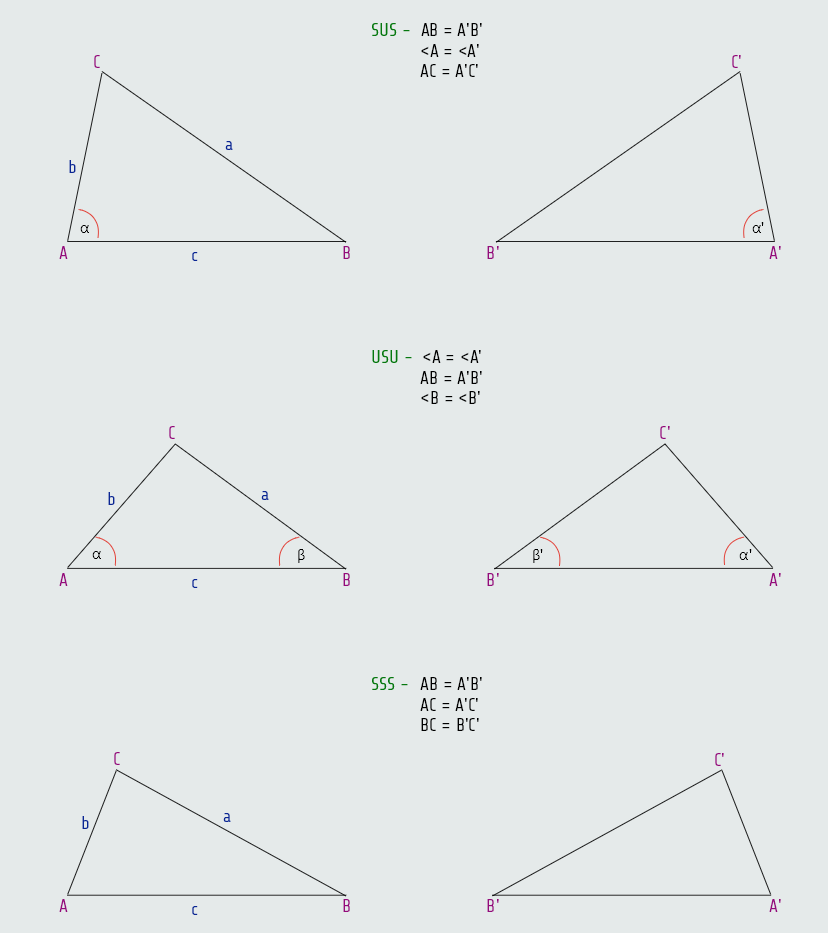
Za stav SSU važi da su dva trougla podudarna ako imaju jednake po dvije stranice i po jedan ugao - i to onaj ugao koji je nasuprot veće stranice.
Dakle, ako za dva trougla ABC i A'B'C' vrijedi:
AB = A'B'
AC = A'C'
--------
AB > AC
--------
∠ ACB = ∠ A'C'B'
kazat' ćemo da su trouglovi ABC i A'B'C' podudarni.