Uglovi sa paralelnim kracima

Definicija: Ako su kraci jednog ugla paralelni sa odgovarajućim kracima drugog ugla, takve uglove nazivamo uglovi sa paralelnim kracima. 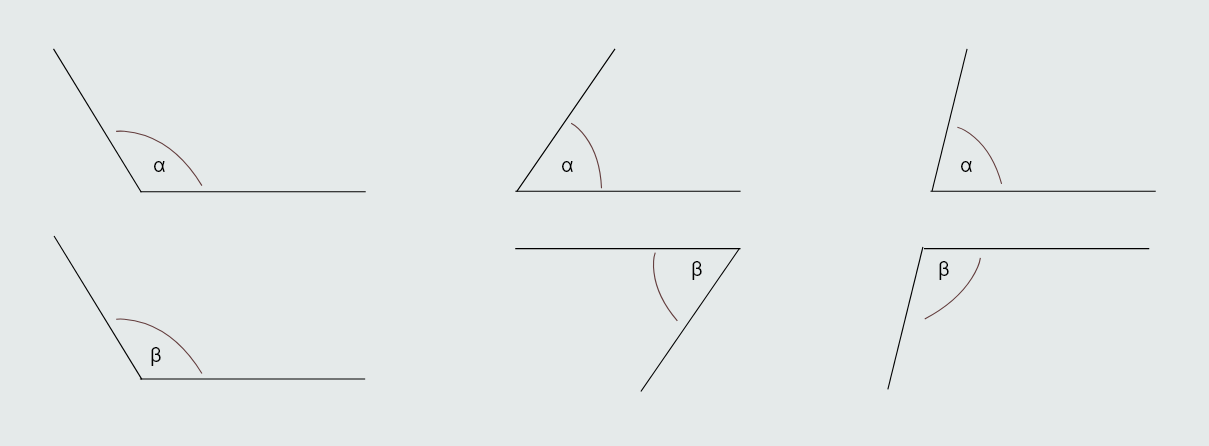Teorema: Dva ugla sa paralelnim kracima su jednaka ako su im kraci jednako ili suprotno usmjereni, a suplementni su ako je jedan par krakova istog a drugi suprotnog smjera.
Na gornjoj slici su prikazani uglovi kod kojih su kraci jednako usmjereni, suprotno usmjereni i na kraju uglovi kod kojih je jedan par krakova jednako, a drugi suprotno usmjeren.
Dokaz pokušajte izvesti koristeći translaciju...

Uglovi sa normalnim kracima

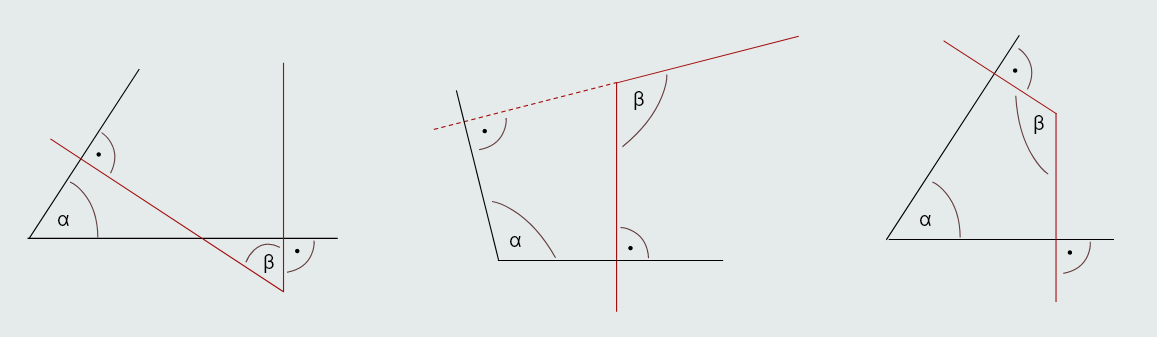
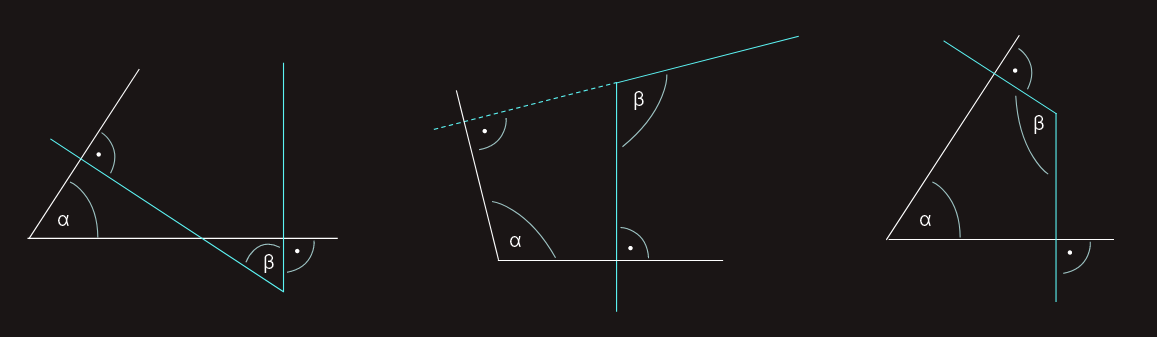
Definicija: Ako su kraci jednog ugla normalni na krake drugog ugla, takve uglove nazivamo uglovi sa normalnim kracima. Teorema: Dva ugla sa normalnim kracima su jednaka ako su oba oštri ili oba tupi, a suplementni su ako je jedan oštar a drugi tup.
Ova tri slučaja su prikazana na gornjoj slici; dokaz pokušajte izvesti koristeći translaciju i rotaciju...

Uglovi na transverzali dviju pravih

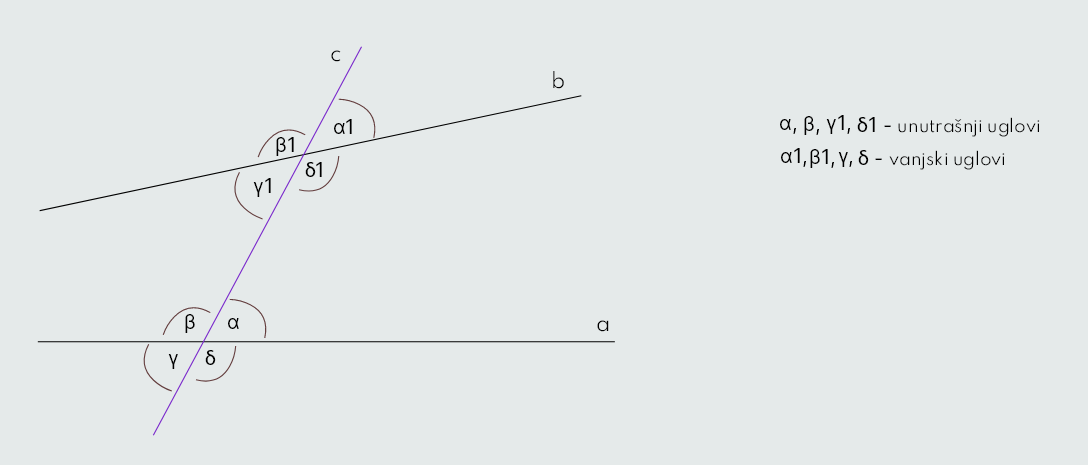
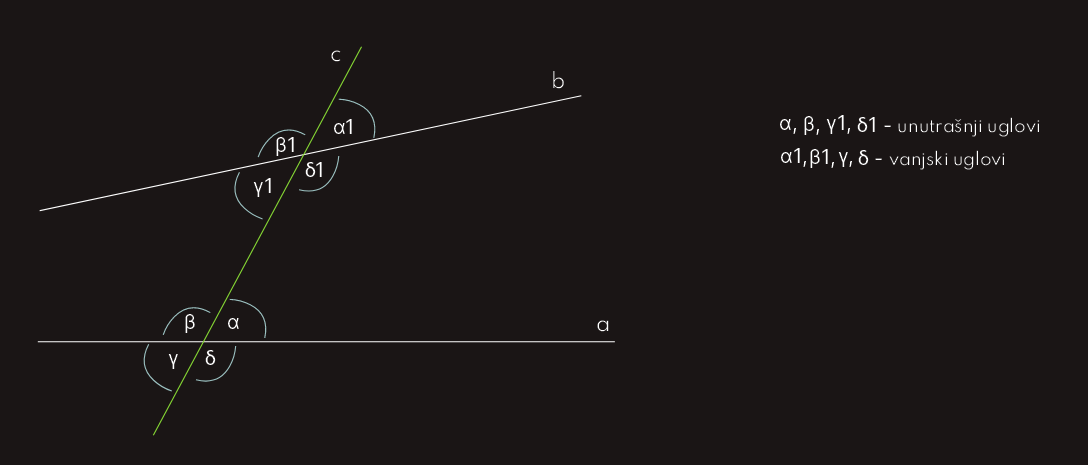
Neka su dvije prave a i b presječene trećom pravom c. Prava c je transverzala pravih a i b; te je na taj način nastalo osam uglova, 4 unutrašnja i 4 vanjska. Definicija: Saglasni uglovi na transverzali dviju pravih su takva dva nesusjedna ugla koji se nalaze sa iste strane transverzale od kojih je jedan unutrašnji, a drugi vanjski.
Dakle, to su uglovi α i α1, β i β1, γ i γ1, δ i δ1.

Definicija: Dva nesusjedna ugla koji se nalaze sa raznih strana transverzale i oba su unutrašnja ili vanjska nazivaju se naizmjenični uglovi.
U našem slučaju to su uglovi: α i γ1, β i δ1, γ i α1, δ i β1.

Definicija: Dva unutrašnja ili dva vanjska ugla koji se nalaze sa iste strane transverzale dviju pravih nazivaju se suprotni uglovi.
Ovdje su to: α i δ1, β i γ1, γ i β1, δ i α1.

Uglovi trougla

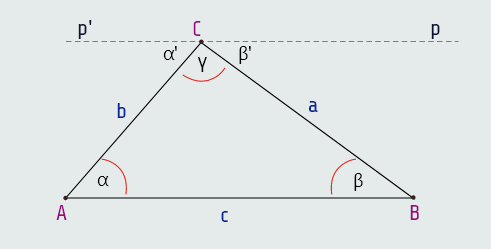
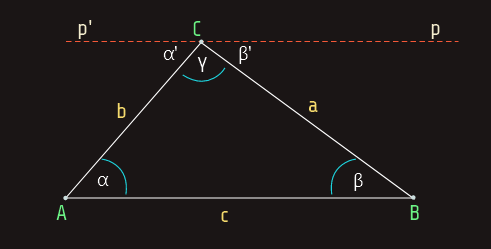
Teorema: Za unutrašnje uglove α, β i γ trougla vrijedi α + β + γ = 180°.
Dokazom ove teoreme bismo uvidjeli i da uglovi trougla nisu međusobno nezavisni; dva ugla uvijek potpuno određuju treći ugao, te da je i zbir vanjskih uglova trougla 360°.

Teorema: Svaki spoljašnji ugao trougla jednak je zbiru dva unutrašnja njemu nesusjedna ugla tog trougla.
Iz ove teoreme zaključujemo i da je svaki vanjski ugao trougla veći od svakog unutrašnjeg njemu nesusjednog ugla.

Centralna simetrija u ravni

Definicija: Rotacija za 180° naziva se centralna simetrija. Centar rotacije nazivamo centar centralne simetrije.
Centralnom simetrijom se prava preslikava u paralelnu pravu, poluprava u paralelnu polupravu, duž u paralelnu i jednaku duž.

Definicija: Figura koja se centralnom simetrijom preslikava u samu sebe naziva se centralno simetrična figura. Centar ove simetrije nazivamo centar simetrije figure.
Centralno simetrične figure su: duž, prava, kružnica, krug, kvadrat, pravougaonik, ...

Osna simetrija u ravni

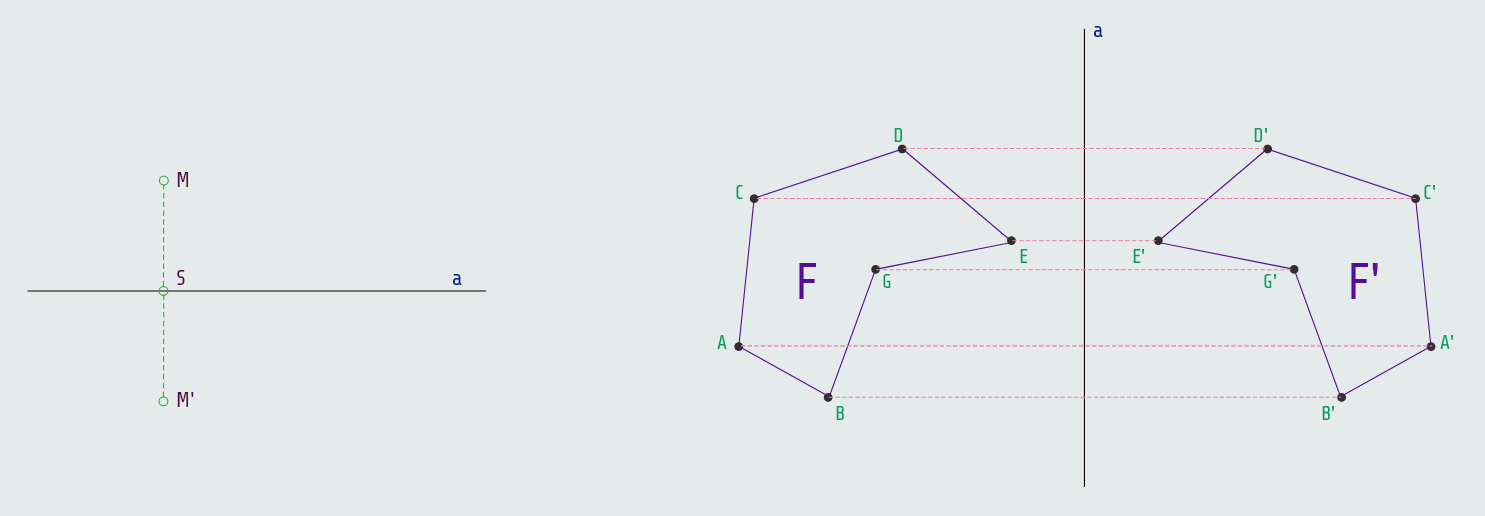
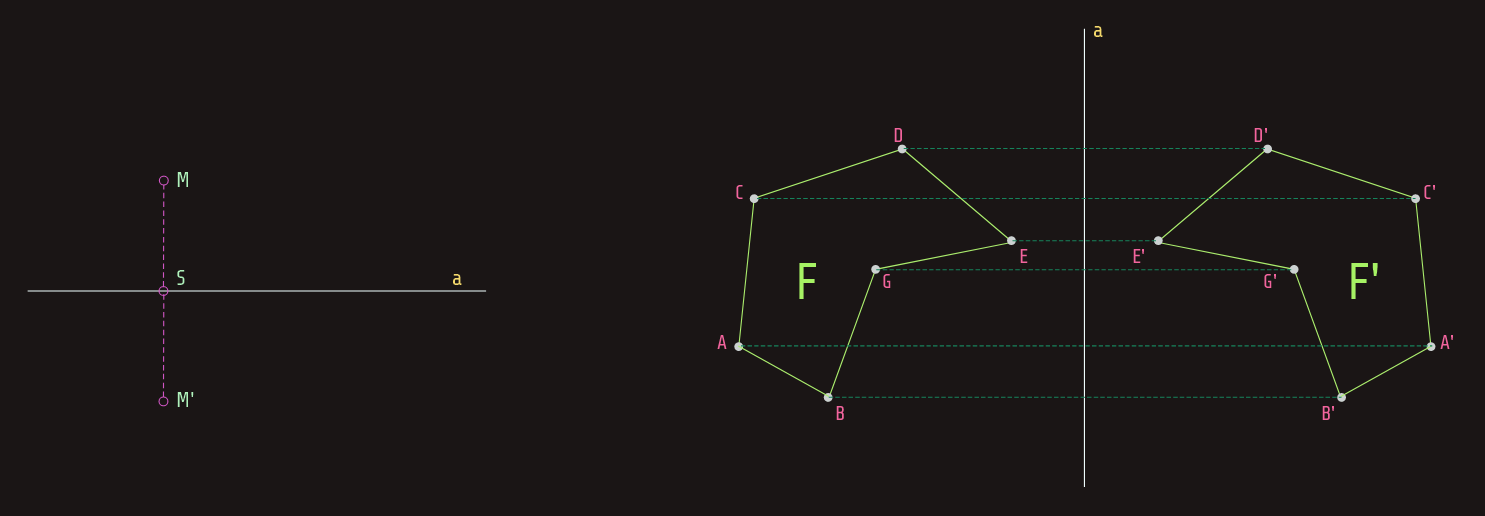
Neka su u ravni dati bilo koja prava a i bilo koja tačka M (gornja slika, lijevo). Neka tačkom M prolazi prava p koja je normalna na pravu a. Presjek pravih a i p označimo sa S. Neka je M' tačka na pravoj p takva da je S središte duži MM'.
Definicija: Za tačke M i M' kažemo da su osno simetrične u odnosu na pravu a ako je prava a normalna na duž MM' u njenom središtu.

Definicija: Transformacija ravni kojom svakoj tački ravni pridružujemo njenu osno simetričnu tačku u odnosu na neku pravu a te ravni, nazivamo osna simetrija u odnosu na pravu a, a pravu a nazivamo osa simetrije.
Na gornjoj desnoj slici se figura F osnom simetrijom transformiše u figuru F', te su ove dvije figure osno simetrične.